如何將二進位制轉換為十進位制？

二進位制是最簡單的數字系統，只使用0和1兩個數字（即基數為2）。由於數位電子技術只有這兩種狀態（0或1），因此二進位制數在現代計算機工程師、網路和通訊專家以及其他專業人士中最受歡迎。

而十進位制數是公眾最熟悉的數字系統。它是基數為10的系統，只有10個符號：0、1、2、3、4、5、6、7、8和9。

從二進位制到十進位制的轉換

主要有兩種方法可以將二進位制數轉換為十進位制數——使用位權法和倍乘法。這些方法解釋如下。

使用位權法

由於數字是位置數字系統的一種。這意味著從右到左的位的權重為20、21、22、23……依此類推，對於整數部分；從左到右的位的權重為2-1、2-2、2-3、2-4……依此類推，對於小數部分。

最高有效位 (MSB)二進位制小數點最低有效位 (LSB)
2221202-12-22-3
4210.50.250.125

假設任何無符號二進位制數為bnb(n-1) ... b1b0.b-1b-2 ... b(m-1)bm。則十進位制數等於二進位制數字 (bn) 乘以它們的2的冪 (2n) 的和，即，bnb(n-1) ... b1b0.b-1b-2 ... b(m-1)bm = bnx2n+b(n-1)x2(n-1)+ ... +b1x21+bx020+b-1x2-1+b-22-2+ ...

這是一個簡單的演算法，您需要將二進位制的位權值乘以其數字，然後將這些步驟的結果相加。

示例1 - 將二進位制數11001010轉換為十進位制數。由於這裡沒有二進位制小數點，也沒有小數部分。

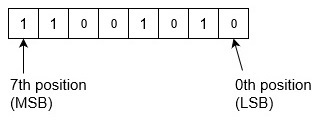
Position

二進位制到十進位制為：

= (11001010)2
= 1x27+1x26+0x25+0x24+1x23+0x22+1x21+0x20
= 128+64+0+0+8+0+2+0
= (202)10

示例2 - 將二進位制數1010.1011轉換為十進位制數。由於這裡有一個二進位制小數點和小數部分。

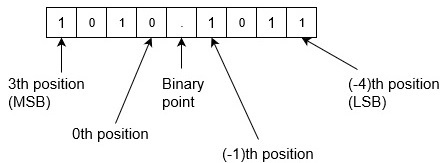
Fractional Part

二進位制到十進位制為：

= (1010.1011)2
= 1x23+0x22+1x21+0x20+1x2-1+0x2-2+1x2-3+1x2-4
= 8+0+2+0+0.5+0+0.125+0.0625
= (10.6875)10

使用倍乘法

這是一種將二進位制數轉換為十進位制數的簡單方法，您需要從輸入的左端數字（或MSB）開始。取最高有效位 (MSB)，寫下，然後乘以2並加上第二個左端位，將其儲存為當前結果，然後再次將當前結果乘以2並加上第三個左端位，將此值更新為當前結果，並繼續此操作，直到加上最低有效位 (LSB 或右端位)。由於每次都在加倍（乘以2），因此此方法稱為倍乘法。

下面分步驟解釋這個簡單的演算法：

  • 寫下二進位制數。

  • 從左開始，將之前的總數乘以2，然後加上當前數字。

  • 將當前總數乘以2，然後加上下一個左端數字。

  • 重複上一步。

例如，將二進位制數11101110轉換為十進位制數。根據上述演算法，二進位制到十進位制為：

= (11101110)2
= 1
= 12+1 =3
= 32+1=7
= 72+0=14
= 142+1=29
= 292+1=59
= 592+1=119
= 1192+0=238
= (238)10

以上是將二進位制數轉換為十進位制數的兩種簡單方法。

更新於：2023年9月14日

24K+ 次瀏覽

開啟你的職業生涯

完成課程並獲得認證

開始學習
廣告