資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學使用C++查詢給定點可以構成四邊形的數量
在歐幾里得平面幾何中，四邊形是由四個頂點和四條邊組成的多邊形。名稱4-gon等包含在四邊形的其他名稱中，有時它們也被稱為正方形、顯示樣式等。
在本文中，我們將解釋從給定點查詢可能四邊形數量的方法。在這個問題中，我們需要找出使用笛卡爾平面中提供的四個點(x, y)可以建立多少個可能的四邊形。以下是給定問題的示例：
Input : A( -2, 8 ), B( -2, 0 ), C( 6, -1 ), D( 0, 8 ) Output : 1 Explanation : One quadrilateral can be formed ( ABCD )
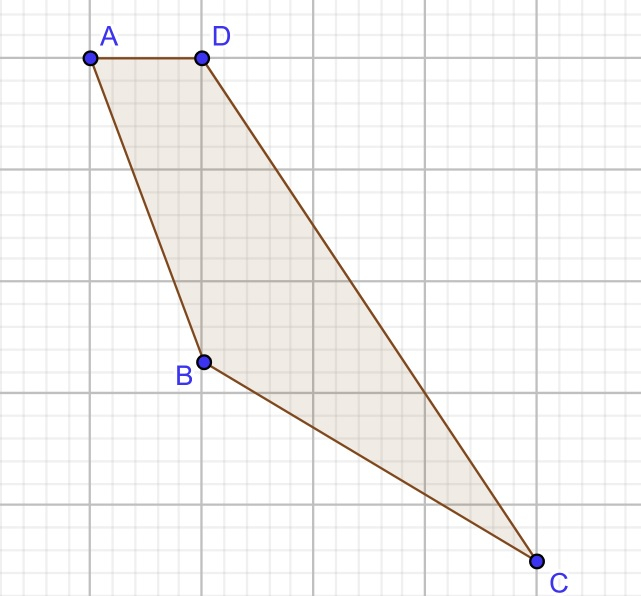
Input : A( 1, 8 ), B( 0, 1 ), C( 4, 0 ), D( 1, 2 ) Output : 3 Explanation : 3 quadrilaterals can be formed (ABCD), (ABDC) and (ADBC).
尋找解決方案的方法
我們將首先檢查4個點中的3個是否共線，如果是，則**無法用這些點構成四邊形**。
之後，我們將檢查4個點中的任意2個是否相同，如果是，則**無法構成四邊形**。
現在，我們將檢查對角線是否相交。如果相交，則只能**構成一個可能的四邊形**，稱為**凸四邊形**。
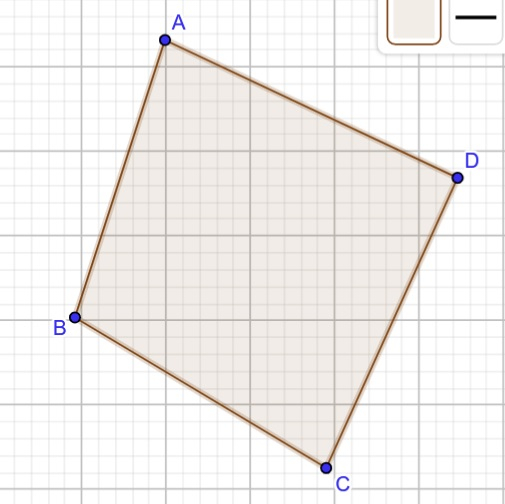
相交總數 = 1
如果對角線不相交，則可以構成三個可能的四邊形，稱為凹四邊形。
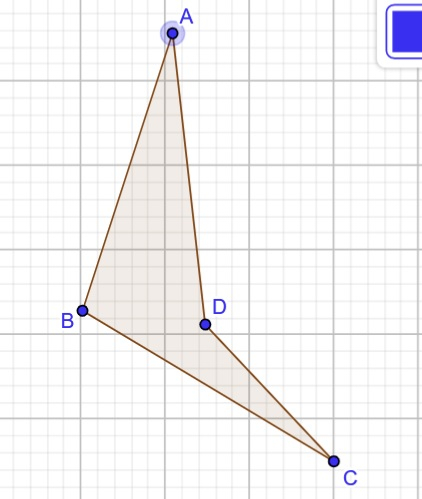
相交總數 = 0
示例
#include <iostream>
using namespace std;
struct Point{ // points
int x;
int y;
};
int check_orientation(Point i, Point j, Point k){
int val = (j.y - i.y) * (k.x - j.x) - (j.x - i.x) * (k.y - j.y);
if (val == 0)
return 0;
return (val > 0) ? 1 : 2;
}
// checking whether line segments intersect
bool check_Intersect(Point A, Point B, Point C, Point D){
int o1 = check_orientation(A, B, C);
int o2 = check_orientation(A, B, D);
int o3 = check_orientation(C, D, A);
int o4 = check_orientation(C, D, B);
if (o1 != o2 && o3 != o4)
return true;
return false;
}
// checking whether 2 points are same
bool check_similar(Point A, Point B){
// If found similiar then we are returning false that means no quad. can be formed
if (A.x == B.x && A.y == B.y)
return false;
// returning true for not found similiar
return true;
}
// Checking collinearity of three points
bool check_collinear(Point A, Point B, Point C){
int x1 = A.x, y1 = A.y;
int x2 = B.x, y2 = B.y;
int x3 = C.x, y3 = C.y;
if ((y3 - y2) * (x2 - x1) == (y2 - y1) * (x3 - x2))
return false;
else
return true;
}
// main function
int main(){
struct Point A,B,C,D;
A.x = -2, A.y = 8;// A(-2, 8)
B.x = -2, B.y = 0;// B(-2, 0)
C.x = 6, C.y = -1;// C(6, -1)
D.x = 0, D.y = 8;// D(0, 8)
// Checking whether any 3 points are collinear
bool flag = true;
flag = flag & check_collinear(A, B, C);
flag = flag & check_collinear(A, B, D);
flag = flag & check_collinear(A, C, D);
flag = flag & check_collinear(B, C, D);
// If points found collinear
if (flag == false){
cout << "Number of quadrilaterals possible from the given points: 0";
return 0;
}
// Checking if 2 points are same.
bool same = true;
same = same & check_similar(A, B);
same = same & check_similar(A, C);
same = same & check_similar(B, D);
same = same & check_similar(C, D);
same = same & check_similar(A, D);
same = same & check_similar(B, C);
// If similiar point exist
if (same == false){
cout << "Number of quadrilaterals possible from the given points: 0";
return 0;
}
// checking whether diagonal intersect or not
flag = true;
if (check_Intersect(A, B, C, D))
flag = false;
if (check_Intersect(A, C, B, D))
flag = false;
if (check_Intersect(A, B, D, C))
flag = false;
if (flag == true)
cout << "Number of quadrilaterals possible from the given points: 3";
else
cout << "Number of quadrilaterals possible from the given points: 1";
return 0;
}輸出
Number of quadrilaterals possible from the given points : 1
以上程式碼的解釋
此程式碼可以透過以下步驟理解：
檢查是否有三個點共線，如果是，則四邊形的數量：0
檢查是否有兩個點相同，如果是，則四邊形的數量：0
檢查是否有任何線段相交
如果是，則四邊形的數量：1
如果不是，則四邊形的數量：3
結論
在本文中，我們解決了從給定的4個點中找到所有可能的四邊形的問題。我們瞭解四邊形的數量如何取決於共線性、相交和方向。我們還為此編寫了C++程式，我們也可以用其他語言（如C、Java和Python）編寫此程式。
更新於：2021年11月24日
360 次瀏覽
廣告