資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究法拉第定律和楞次定律
法拉第電磁感應定律
邁克爾·法拉第（一位英國科學家）進行了一系列實驗來演示電磁感應現象，並將他的結論總結成兩個定律，稱為法拉第電磁感應定律。
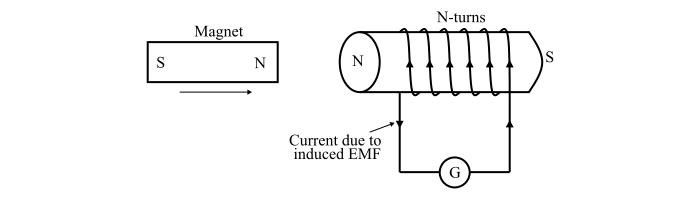
電磁感應第一定律
第一定律指出“當穿過導體或線圈的磁通量發生變化時，導體或線圈中就會感應出電動勢”。因此，第一定律說明了在什麼條件下導體或線圈中會感應出電動勢。
電磁感應第二定律
第二定律指出“導體或線圈中感應電動勢的大小與磁通量變化率成正比”。因此，第二定律給出了導體或線圈中感應電動勢的大小。
解釋 - 考慮一個具有 N 個匝數的線圈，並且穿過該線圈的磁通量在 t 秒內從 $\varphi_{1}$ 變為 $\varphi_{2}$。因此，
$$\mathrm{初始磁通鏈數,ψ_{1} = N\varphi_{1}}$$
$$\mathrm{最終磁通鏈數, ψ_{2} = N\varphi_{2}}$$
$$\mathrm{\therefore 感應電動勢,e\propto\frac{ψ_2-ψ_1}{t}\propto\frac{N\varphi_2-N\varphi_1}{t}}$$
$$\mathrm{\Longrightarrow e=k(\frac{N\varphi_2-N\varphi_1}{t})}$$
其中 k 是比例常數，在 SI 單位中其值為 1。因此，
$$\mathrm{\Longrightarrow e=(\frac{N\varphi_2-N\varphi_1}{t})}$$
微分形式為：
$$\mathrm{e=N\frac{d\varphi}{dt}}$$
上述公式從數學上表示了法拉第第二定律。
楞次定律
一位德國科學家，埃米爾·楞次，給出了一個確定導體或線圈中電磁感應感應電動勢方向的規則，其陳述如下：
“感應電動勢產生的電流的方向將與產生它的原因相反，即感應電動勢產生的電流將建立一個磁通量來抵消產生它的磁通量變化”。
數學上，楞次定律透過在法拉第第二定律的右側新增一個負號來表示，即
$$\mathrm{e=-N\frac{d\varphi}{dt}}$$
這裡，負號表示感應電動勢與感應它的變化磁場相反。因此，楞次定律直接遵循能量守恆定律，即為了線上圈或導體中感應出電動勢，必須在阻力中消耗一些能量。
數值示例
一個 600 匝線圈與 25 mWb 的磁通量相關聯。如果此磁通量在 3 毫秒內反向，則計算線圈中感應的電動勢。
解答
$$\mathrm{磁通量變化,d\varphi=\varphi_{2} - \varphi_{1}=25-(-25)=50nmb}$$
$$\mathrm{變化所需時間,dt=3ms}$$
$$\mathrm{\therefore 感應電動勢,e = N\frac{d\varphi}{dt}=600\times(\frac{50\times10^{-3}{3}}\times10^{-3})=10000=10kV}$$
543 次瀏覽
