解釋兩個有限狀態機之間的等價性。
如果兩個有限自動機 (FA) 接受輸入集 Σ 上的相同字串集,則稱這兩個有限自動機等價。
當兩個 FA 等價時,存在一個輸入集 Σ 上的字串 x。如果一個 FA 在接受該字串後到達最終狀態,則另一個 FA 也到達最終狀態。
方法
下面解釋了比較兩個 FA 的方法:
令 M 和 M1 為兩個 FA,Σ 為輸入字串集。
步驟 1 - 構造一個狀態轉移表,其中包含成對的條目 (q, q1),其中 q ∈ M 且 q1 ∈ M1,對應每個輸入符號。
步驟 2 - 如果我們得到一個對,其中一個為最終狀態,另一個為非最終狀態,那麼我們終止狀態轉移表的構造,並宣告這兩個 FA 不等價。
步驟 3 - 當狀態轉移表中不再出現新的對時,狀態轉移表的構造終止。
示例
考慮兩個確定性有限自動機 (DFA),並檢查它們是否等價。
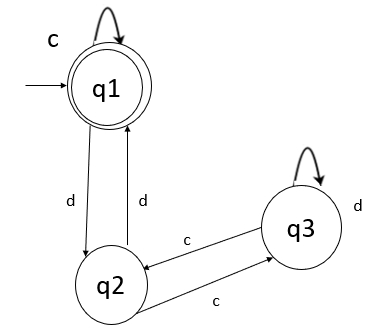
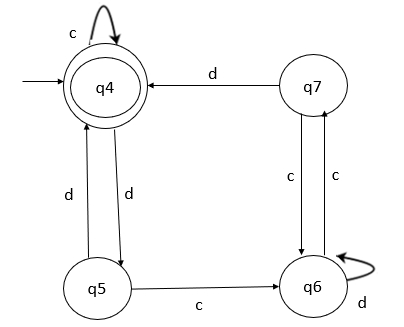
解釋
- 步驟 1 - 首先,為每個輸入 c 和 d 構造狀態轉移表。
- 步驟 2 - 從第一個機器 M 在狀態 q1 接收輸入 c 時,我們僅到達狀態 q1,它是最終狀態。
- 步驟 3 - 從第二個機器 M1 在狀態 q4 接收輸入 c 時,我們到達狀態 q4,它是最終狀態。
- 步驟 4 - 因此,對於輸入 c 的狀態 (q1, q4),我們得到下一個狀態為 (q1, q4)。兩者都是最終狀態。
- 步驟 5 - 同樣,對於狀態 (q1, q4) 的輸入 d,我們得到下一個狀態為 (q2, q5)。兩者都是中間狀態。因此,兩個機器中的第一個狀態是相等的。
- 步驟 6 - 同樣,我們對兩個機器中的其餘狀態執行此操作。
- 步驟 7 - 在一對狀態中,如果兩者都是最終狀態或兩者都是非最終狀態,那麼我們可以說這兩個 DFA 等價,讓我們檢查其餘部分。
狀態轉移表如下所示:
| 狀態 | c | d |
|---|---|---|
| {q1,q4} | {q1, q4} FS FS | {q2, q5} IS IS |
| {q2,q5} | {q3, q6} IS IS | {q1, q4} FS FS |
| {q3, q6} | {q2, q7} IS IS | {q3, q6} IS IS |
| {q2, q7} | {q3, q6} IS IS | {q1, q4} FS FS |
這裡,FS 是最終狀態,IS 是中間狀態。
因此,透過檢視上表,很明顯我們在一對中沒有得到一個最終狀態和一箇中間狀態。因此,我們可以宣告這兩個 DFA 等價。

廣告

 資料結構
資料結構 網路
網路 關係資料庫管理系統
關係資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 語言程式設計
C 語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP