資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究解釋計算理論中語法的概念
在計算理論中，語法是一組生成句法正確的句子的形式規則的有限集合。
語法的正式定義是，它被定義為四個元組：
G=(V,T,P,S)
G 是一個語法，它包含一組產生式規則。它用於生成語言的字串。
T 是終結符的最終集合。它用小寫字母表示。
V 是非終結符的最終集合。它用大寫字母表示。
P 是一組產生式規則，用於用字串中的其他終結符（產生式的右側）替換非終結符（產生式的左側）。
S 是用於推匯出字串的起始符號。
語法由兩個基本元素組成
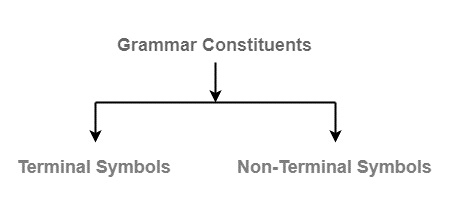
終結符 - 終結符是使用語法生成的句子的組成部分，並使用小寫字母（如 a、b、c 等）表示。
非終結符 - 非終結符參與句子的生成，但不是句子的組成部分。這些型別的符號也稱為輔助符號和變數。它們用大寫字母（如 A、B、C 等）表示。
示例 1
考慮一個語法
G = (V , T , P , S)
其中，
V = { S , A , B } ⇒ Non-Terminal symbols
T = { a , b } ⇒ Terminal symbols
Production rules P = { S → ABa , A → BB , B → ab , AA → b }
S = { S } ⇒ Start symbol示例 2
考慮一個語法
G=(V,T,P,S)
其中，
V= {S, A, B} ⇒ non terminal symbols
T = { 0,1} ⇒ terminal symbols
Production rules P = { S→A1B
A→0A| ε
B→0B| 1B| ε }
S= {S} ⇒ start symbol.語法的型別
不同型別的語法：
| 語法 | 語言 | 自動機 | 產生式規則 |
|---|---|---|---|
| 0 型 | 遞迴可列舉 | 圖靈機 | 無限制 |
| 1 型 | 上下文相關 | 線性界限非確定性機器 | αAβ→αγβ |
| 2 型 | 上下文無關 | 非確定性下推自動機 | A→γ |
| 3 型 | 正則 | 有限狀態自動機 | A→αB A→α |
表示語法型別在計算理論 (TOC) 中的圖如下：
更新於: 2023-11-01
42K+ 次檢視
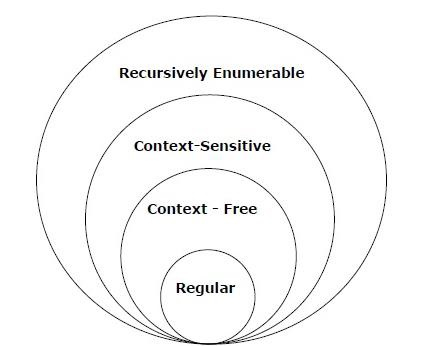
廣告