在一個班級的35名學生的體檢中，記錄了他們的體重如下

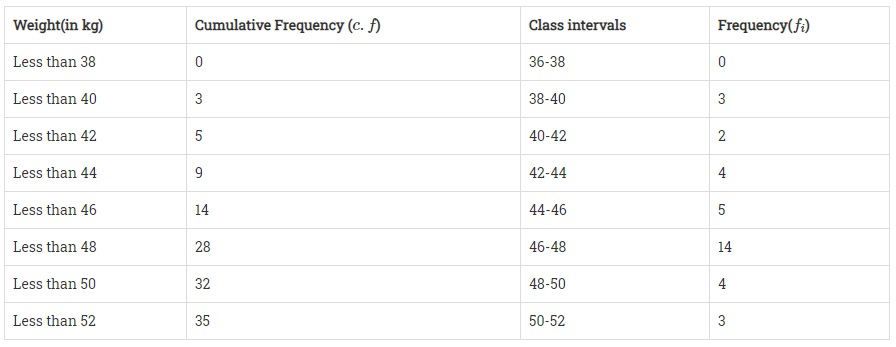
體重（公斤）	學生人數
小於38	0
小於40	3
小於42	5
小於44	9
小於46	14
小於48	28
小於50	32
小於52	35

根據給定資料繪製小於型累積頻數曲線。由此從圖中得出中位數體重，並用公式驗證結果。

---

已知

在一個班級的35名學生的體檢中，記錄了他們的體重。

任務

我們必須根據給定資料繪製小於型累積頻數曲線，並從圖中得出中位數體重，並用公式驗證結果。

解答

我們首先按照以下方法準備小於型累積頻數分佈表

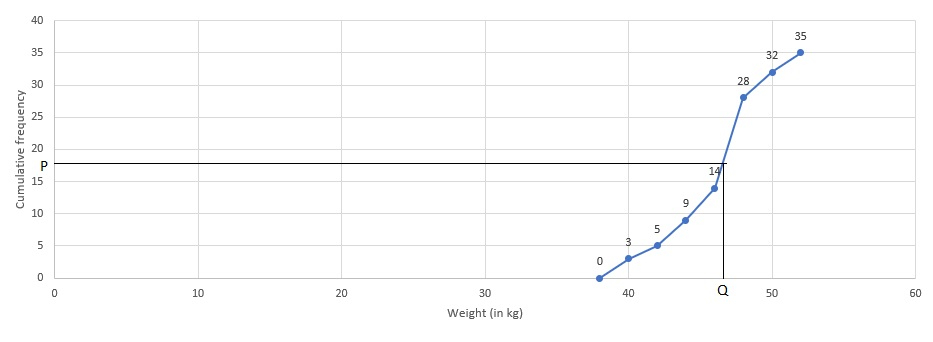
將體重表示在X軸上，將累積頻數表示在Y軸上。

在圖上繪製點 (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32), (52, 35)，並用手繪線將它們連線起來，得到如圖所示的累積頻數曲線。

這裡，

$N = 35$

$\frac{N}{2}=\frac{35}{2}=17.5$

從Y軸上的點 $P$ (17.5) 畫一條平行於X軸的線，與曲線相交，然後畫一條平行於Y軸的線，與X軸在 $Q$ 點相交。

從圖中，中位數約為 46.5 公斤。

因此，
46-48 是中位陣列
這裡，

$l= 46, h = 2,f= 14, F= 14$

這意味著，

中位數 $=l+\frac{\frac{N}{2}-F}{f} \times h$

$=46+\frac{17.5-14}{14} \times 2$

$=46+\frac{3.5 \times 2}{14}$

$=46+0.5$

$=46.5$

因此驗證。