在數軸上畫出下列有理數
$(i)$. $\frac{3}{4}$
$(ii)$. $\frac{-5}{8}$
$(iii)$. $\frac{-7}{4}$
$(iv)$. $\frac{7}{8}$
已知：有理數
$(i)$. $\frac{3}{4}$
$(ii)$. $\frac{-5}{8}$
$(iii)$. $\frac{-7}{4}$
$(iv)$. $\frac{7}{8}$
要求：在數軸上畫出給定的有理數。
解答：以下是給定有理數在數軸上的表示
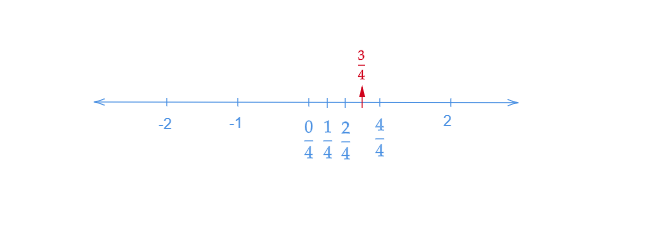
$(i)$. $\frac{3}{4}$在數軸上的表示
讓我們畫一條數軸。我們知道$\frac{3}{4}$小於$1$。所以，它位於$0$和$1$之間。
讓我們將數軸從$0$到$1$分成四個相等的部分。
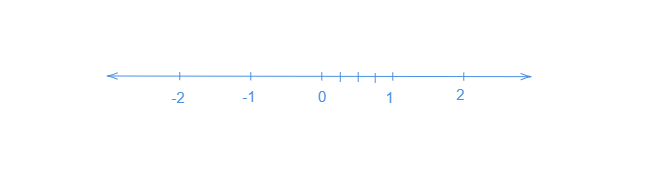
讓我們在數軸上表示$\frac{0}{4},\ \frac{1}{4},\ \frac{2}{4}$和$\frac{3}{4}$。其中$\frac{0}{4}$表示$0$，$\frac{4}{4}$表示$1$。
在數軸上標出$\frac{3}{4}$。
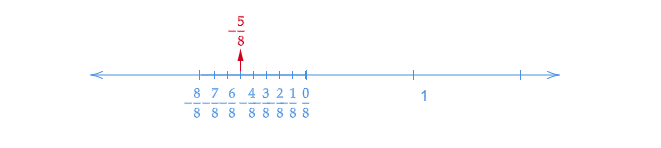
$(ii)$. $\frac{-5}{8}$在數軸上的表示
讓我們畫一條數軸。我們知道$-\frac{5}{8}$大於$-1$。所以，它位於$0$和$-1$之間。
讓我們將數軸從$0$到$-1$分成八個相等的部分。
讓我們在數軸上表示$\frac{0}{8},\ -\frac{1}{8},\ -\frac{2}{8},\ -\frac{3}{8},\ -\frac{4}{8},\ -\frac{5}{8},\ -\frac{6}{8},\ -\frac{7}{8}$和$-\frac{8}{8}$。其中$\frac{0}{8}$表示$0$，$-\frac{8}{8}$表示$-1$。
在數軸上標出$-\frac{5}{8}$。
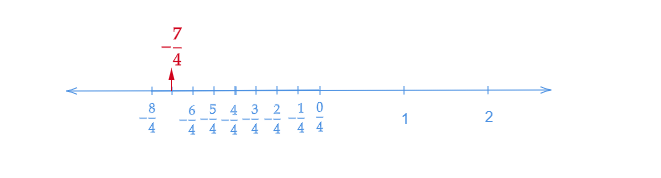
$(iii)$. $\frac{-7}{4}$在數軸上的表示
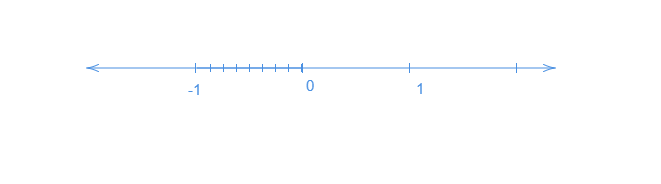
讓我們畫一條數軸。我們知道$-\frac{7}{4}$小於$-1$且大於$-2$。所以，它位於$-1$和$-2$之間。
讓我們將數軸從$0$到$-2$分成八個相等的部分。
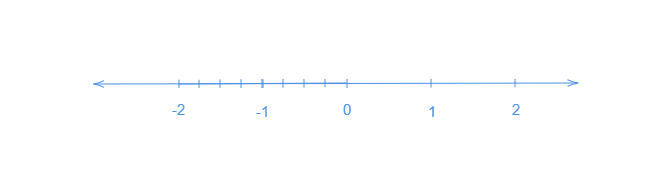
讓我們在數軸上表示$\frac{0}{4},\ -\frac{1}{4},\ -\frac{2}{4},\ -\frac{3}{4},\ -\frac{4}{4},\ -\frac{5}{4},\ -\frac{6}{4},\ -\frac{7}{4}$和$-\frac{8}{4}$。其中$\frac{0}{4}$表示$0$，$-\frac{8}{4}$表示$-2$。
在數軸上標出$-\frac{7}{4}$。
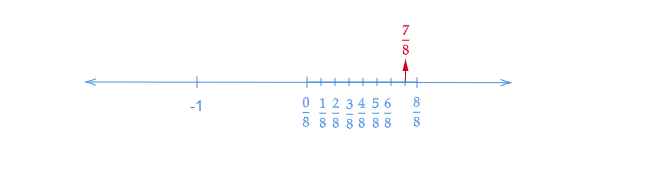
$(iv)$. $\frac{7}{8}$在數軸上的表示
讓我們畫一條數軸。我們知道$\frac{7}{8}$小於$1$。所以，它位於$0$和$1$之間。
讓我們將數軸從$0$到$1$分成八個相等的部分。
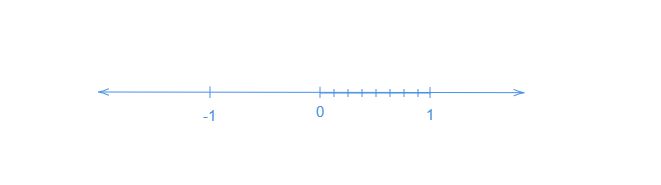
讓我們在數軸上表示$\frac{0}{8},\ \frac{1}{8},\ \frac{2}{8},\ \frac{3}{8},\ \frac{4}{8},\ \frac{5}{8},\ \frac{6}{8},\ \frac{7}{8}$和$\frac{8}{8}$。其中$\frac{0}{8}$表示$0$，$\frac{8}{8}$表示$1$。
在數軸上標出$\frac{7}{8}$。
- 相關文章
- 將下列有理數相加：(i) \( \frac{-5}{7} \) 和 \( \frac{3}{7} \)(ii) \( \frac{-15}{4} \) 和 \( \frac{7}{4} \)(iii) \( \frac{-8}{11} \) 和 \( \frac{-4}{11} \)(iv) \( \frac{6}{13} \) 和 \( \frac{-9}{13} \)
- 利用有理數加法的交換律和結合律，將下列各數表示成有理數：(i) \( \frac{2}{5}+\frac{7}{3}+\frac{-4}{5}+\frac{-1}{3} \)(ii) \( \frac{3}{7}+\frac{-4}{9}+\frac{-11}{7}+\frac{7}{9} \)(iii) \( \frac{2}{5}+\frac{8}{3}+\frac{-11}{15}+\frac{4}{5}+\frac{-2}{3} \)(iv) \( \frac{4}{7}+0+\frac{-8}{9}+\frac{-13}{7}+\frac{17}{21} \)
- 求下列各分數的倒數。(i) $\frac{5}{8}$(ii) $\frac{8}{7}$(iii) $\frac{13}{7}$(iv) $\frac{3}{4}$
- 將下列有理數相加：(i)M/b> \( \frac{3}{4} \) 和 \( \frac{-5}{8} \)(ii) \( \frac{5}{-9} \) 和 \( \frac{7}{3} \)(iii) \( -3 \) 和 \( \frac{3}{5} \)(iv) \( \frac{-7}{27} \) 和 \( \frac{11}{18} \)(v) \( \frac{31}{-4} \) 和 \( \frac{-5}{8} \)(vi) \( \frac{5}{36} \) 和 \( \frac{-7}{12} \)(vii) \( \frac{-5}{16} \) 和 \( \frac{7}{24} \)(viii) \( \frac{7}{-18} \) 和 \( \frac{8}{27} \)
- 在數軸上表示下列各數 (i) $\frac{-4}{7}$(ii) $\frac{-2}{5}$
- 在數軸上表示下列各數。(i) \( \frac{7}{4} \) (ii) \( \frac{-5}{6} \).
- 化簡下列各數並寫成有理數的形式：(i) \( \frac{3}{4}+\frac{5}{6}+\frac{-7}{8} \)(ii) \( \frac{2}{3}+\frac{-5}{6}+\frac{-7}{9} \)(iii) \( \frac{-11}{2}+\frac{7}{6}+\frac{-5}{8} \)(iv) \( \frac{-4}{5}+\frac{-7}{10}+\frac{-8}{15} \)(v) \( \frac{-9}{10}+\frac{22}{15}+\frac{13}{-20} \)(vi) \( \frac{5}{3}+\frac{3}{-2}+\frac{-7}{3}+3 \)
- 畫數軸並在其上定位點：(a) \( \frac{1}{2}, \frac{1}{4}, \frac{3}{4}, \frac{4}{4} \)(b) \( \frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{7}{8} \)(c) \( \frac{2}{5}, \frac{3}{5}, \frac{8}{5}, \frac{4}{5} \)
- 求：(i) $12\div\frac{3}{4}$(ii) $14\div\frac{5}{6}$(iii) $8\div\frac{7}{3}$(iv) $4\div\frac{8}{3}$(v) $3\div2\frac{1}{3}$(vi) $5\div3\frac{4}{7}$
- 在下列各組中，從第二個有理數中減去第一個有理數：(i) \( \frac{3}{8}, \frac{5}{8} \)(ii) \( \frac{-7}{9}, \frac{4}{9} \)(iii) \( \frac{-2}{11}, \frac{-9}{11} \)(iv) \( \frac{11}{13}, \frac{-4}{13} \)(v) \( \frac{1}{4}, \frac{-3}{8} \)(vi) \( \frac{-2}{3}, \frac{5}{6} \)(vii) \( \frac{-6}{7}, \frac{-13}{14} \)(viii) \( \frac{-8}{33}, \frac{-7}{22} \)
- 計算：(i) $3-\frac{2}{5}$(ii) $4+\frac{7}{8}$(iii) $\frac{3}{5}+\frac{2}{7}$(iv) $\frac{9}{11}-\frac{4}{15}$(v) $\frac{7}{10}+\frac{2}{5}+\frac{3}{2}$(vi) $2\frac{2}{3}+3\frac{1}{2}$(vii) $8\frac{1}{2}-3\frac{5}{8}$
- 驗證下列每對有理數加法的交換律：(i) \( \frac{-11}{5} \) 和 \( \frac{4}{7} \)(ii) \( \frac{4}{9} \) 和 \( \frac{7}{-12} \)(iii) \( \frac{-3}{5} \) 和 \( \frac{-2}{-15} \)(iv) \( \frac{2}{-7} \) 和 \( \frac{12}{-35} \)(v) 4 和 \( \frac{-3}{5} \)(vi) \( -4 \) 和 \( \frac{4}{-7} \)
- 化簡：(i) \( \frac{-3}{2}+\frac{5}{4}-\frac{7}{4} \)(ii) \( \frac{5}{3}-\frac{7}{6}+\frac{-2}{3} \)(iii) \( \frac{5}{4}-\frac{7}{6}-\frac{-2}{3} \)(iv) \( \frac{-2}{5}-\frac{-3}{10}-\frac{-4}{7} \)(v) \( \frac{5}{6}+\frac{-2}{5}-\frac{-2}{15} \)(vi) \( \frac{3}{8}-\frac{-2}{9}+\frac{-5}{36} \)
- 將下列各數表示成$\frac{p}{q}$形式的有理數(i) \( -\frac{8}{3}+\frac{-1}{4}+\frac{-11}{6}+\frac{3}{8}-3 \)(ii) \( \frac{6}{7}+1+\frac{-7}{9}+\frac{19}{21}+\frac{-12}{7} \)(iii) \( \frac{15}{2}+\frac{9}{8}+\frac{-11}{3}+6+\frac{-7}{6} \)(iv) \( \frac{-7}{4}+0+\frac{-9}{5}+\frac{19}{10}+\frac{11}{14} \)(v) \( \frac{-7}{4}+\frac{5}{3}+\frac{-1}{2}+\frac{-5}{6}+2 \)
- 給出下列有理數的等價有理數：$(i)$. $\frac{-2}{7}$$(ii)$. $\frac{5}{-3}$$(iii)$. $\frac{4}{9}$
資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究