位移電流

---

介紹

最初，電和磁被視為獨立的學科。後來，由於奧斯特、法拉第、麥克斯韋等人的貢獻，它們發展成為一個統一的學科。載流導線在其周圍產生磁場。法拉第透過他的實驗表明，即使電路中沒有電池，也可以產生電流。磁場的變化可以在電路中產生電流。這個結果被稱為電磁感應。麥克斯韋試圖以統一和緊湊的方式寫出電磁學的所有主要方程。這些方程被稱為麥克斯韋方程組。

這組方程包括：靜電的高斯定理、磁的高斯定理、安培環路定理和法拉第電磁感應定律。麥克斯韋發現安培定律存在一些不一致之處。他修改了這個方程，並引入了一個新的概念，稱為位移電流。因此，這個方程有時也被稱為麥克斯韋-安培方程。

什麼是位移電流？

詹姆斯·克拉克·麥克斯韋引入了這個概念。如果在一個區域內有電荷流動且存在電流，那麼由於電流的存在，就會產生磁場。根據麥克斯韋的理論，在空間中，磁場是由位移電流產生的。與傳統電流不同，它不是由電荷組成的。由於電容器極板之間存在自由空間，我們可以透過以電容器為例來推匯出位移電流的表示式。

位移電流方程

為了得到位移電流方程，我們以電容器為例。我們嘗試使用安培定律來求解磁場 -

$$\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=\mu _{0}i_{enc}}$$

其中 B = 磁場，i = 透過表面的淨電流。

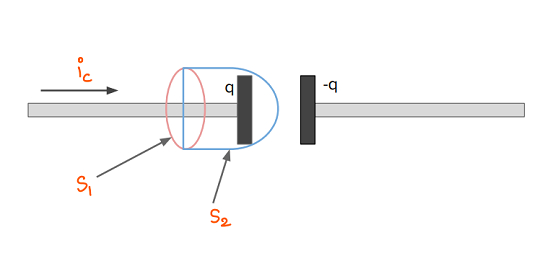
首先，我們嘗試透過取表面 $\mathrm{S_{1}}$ 來計算磁場。透過該表面的電流為 $\mathrm{i_{c}}$。因此，根據安培定律，將存在一些磁場。如果我們取表面 $\mathrm{S_{2}}$，那麼將沒有電流透過該表面。這意味著 $\mathrm{\overrightarrow{B}.\overrightarrow{dl}}$ 同時為零和非零。這是一個矛盾的結果。

麥克斯韋透過引入位移電流解決了這個問題。

$$\mathrm{i_{d}=\epsilon _{0}\frac{d \phi _{E}}{dt}}$$

這裡 $\mathrm{i_{d}}$= 位移電流

$\mathrm{\phi _{E}}$ = 電通量

我們可以將此項包含在安培定律中。

$$\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=\mu _{0}(i_{c}+i_{d})=\mu _{0}i_{c}+\mu _{0}\epsilon _{0}\frac{d\phi _{E}}{dt}}$$

它被稱為麥克斯韋-安培方程。

如果我們使用此關係，我們可以解決電容器問題中產生的歧義。

對於表面 $\mathrm{S_{1}:i=i_{c}}$ 且 $\mathrm{i_{d}=0}$，因為電通量沒有變化。

對於表面 $\mathrm{S_{2}:i=i_{d}}$ 且 $\mathrm{i_{c}=0}$，因為沒有電荷。

因此，現在兩個表面的磁場將不為零。

位移電流的特性

位移電流是由變化的電通量產生的。它可以寫成 -

$$\mathrm{i_{d}=\epsilon _{0}\frac{d\phi _{E}}{dt}}$$

它具有以下特性 -

• 它是向量量。

• 它以安培為單位測量，其量綱與傳統電流相似。

• 它不是由電子的流動產生的，而是由電場的變化產生的。

• 它不遵循歐姆定律。

• 對於閉合路徑，它為零。

• 它不是實際電流。

位移電流的應用

我們可以使用位移電流計算圓形電容器內部的磁場。

假設電容器極板的半徑為 R，然後我們想象在這些極板之間有一根半徑為 R 的圓形導線。我們將流過導線的電流等於位移電流 $\mathrm{i_{d}}$。我們可以在此處使用安培環路定律。由於極板之間只有位移電流 -

$$\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=B\oint dl=B2\pi r}$$

r= 磁場點到中心的距離。

電流均勻分佈，環路包圍的電流 $\mathrm{i_{enc}}$ 與環路包圍的面積成正比。因此

$$\mathrm{i_{enc}=i_{d}\frac{\pi r^{2}}{\pi R^{2}}}$$

這意味著

$$\mathrm{B2\pi r=\mu _{0}i_{enc}}$$

$$\mathrm{B2\pi r=\mu _{0}i_{d}\frac{\pi r^{2}}{\pi R^{2}}}$$

$$\mathrm{B=(\frac{\mu _{0}i_{d}}{2\pi R^{2}})r}$$

它是電容器內部的磁場。它與電容器極板半徑的平方成反比，與磁場點到中心的距離成正比。

我們還可以計算圓形電容器外部的磁場，它將是 -

$$\mathrm{B=\frac{\mu _{0}i_{d}}{2\pi r}}$$

結論

麥克斯韋發現安培定律存在一些不一致之處。他透過引入一種稱為位移電流的電流修改了該方程。位移電流不是由電荷的流動產生的，而是由變化的電通量產生的。它的單位和量綱與傳統電流相同。

常見問題解答

Q1. 寫下麥克斯韋電磁方程組。

答：麥克斯韋電磁方程組如下 -

• $\mathrm{\oint \overrightarrow{E}.\overrightarrow{dA}=\frac{q_{enc}}{\epsilon _{0}}}$，它將淨電荷與電通量聯絡起來。

• $\mathrm{\oint \overrightarrow{E}.\overrightarrow{dA}=0}$，它將淨磁荷與磁通量聯絡起來。

• $\mathrm{\oint \overrightarrow{E}.\overrightarrow{dA}=-\frac{d\phi _{B}}{dt}}$，它將磁通量的變化與感應電場聯絡起來。

• $\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=\mu _{0}i_{c}+\mu _{0}\epsilon _{0}\frac{d\phi _{E}}{dt}}$，它將感應磁場與電流聯絡起來。

Q2. 半徑為 2cm 的圓形電容器的位移電流為 4A，求電容器內部距離 R/4 處的磁場。

答：已知 R = 2cm = $\mathrm{2\times 10^{-2}m}$

$$\mathrm{I = 4A}$$

$$\mathrm{r=\frac{R}{4}}$$

我們可以使用我們在上一節中推匯出的公式 -

$$\mathrm{B=(\frac{\mu _{0}i_{d}}{2\pi R^{2}})r}$$

$$\mathrm{B=\frac{4\pi \times 10^{-7}\times 4}{2\pi \times R^{2}}\frac{R}{4}=\frac{2\times 10^{-7}\times 4}{R\times 4}}$$

$$\mathrm{B=\frac{2\times 10^{-7}}{2 \times 10^{-2}}=10^{-5}}$$

$$\mathrm{B=10^{-5}T}$$

Q3. 說明安培環路定理。

答：安培定律可以這樣陳述：“穿過任何包含穩恆電流的閉合迴路的磁場力的線積分與穿過該回路的電流成正比。”

假設存在一個閉合路徑 C，並且穿過它的淨電流為 $\mathrm{i_{enc}}$。然後我們可以寫

$$\mathrm{\oint \overrightarrow{B}.\overrightarrow{dl}=\mu _{0}i_{enc}}$$

Q4. 一個平行板電容器的電勢為 100 V。如果極板之間的距離為 $\mathrm{}$𝟐。計算 $\mathrm{}$ 的位移電流。

答：平行板電容器的電勢 V = 100V

極板之間的距離 d = 2mm = $\mathrm{2\times 10^{-3}mm}$

$$\mathrm{極板面積 A\:=\:20\times 10^{-4}m^{2}}$$

$$\mathrm{時間 t=2μs=2\times 10^{-6}s}$$

$$\mathrm{位移電流 i_{d}=\epsilon _{0}\frac{d\phi }{dt}=\epsilon _{0}\frac{EA}{t}}$$

我們知道 $\mathrm{E=\frac{v}{d} }$

$$\mathrm{因此，i_{d}=\epsilon _{0}\frac{vA }{dt}=8.85\times 10^{-12}\frac{10^{2}\times 20\times 10^{-4}}{2\times 10^{-3}\times 10^{-6}\times 2 }}$$

$$\mathrm{i_{d}=\frac{8.85\times 5\times 10^{-16}}{10^{-9}}=8.85\times 5\times 10^{-7}}$$

$$\mathrm{i_{d}=44.25\times 10^{-7}A}$$

$$\mathrm{i_{d}=4.4μA}$$

Q5. 位移電流的存在是否需要電場的變化？

答：如果電通量發生變化，則可能存在位移電流。在某些情況下，電場可能沒有變化，但總通量卻在變化。