資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學感應電動機圓圖的繪製
感應電動機圓圖
圓圖是感應電動機效能的圖形表示。它對於研究感應電動機在所有執行條件下的效能非常有用。感應電動機圓圖的繪製基於電動機的等效電路，如圖1所示。
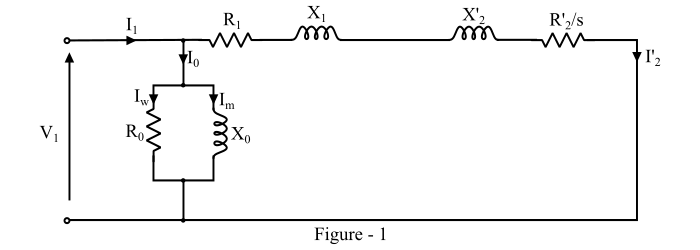
透過在等效電路中應用基爾霍夫電流定律 (KCL)，我們可以寫出：
$$\mathrm{𝐼_1 = 𝐼_0 + 𝐼′_2 … (1)}$$
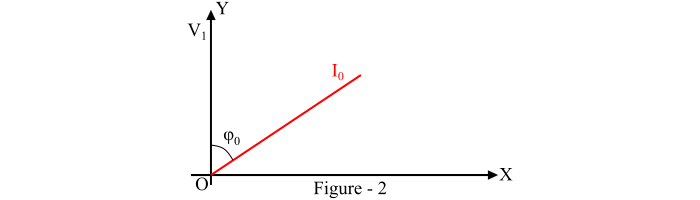
如果將相電壓V1沿OY的垂直軸線取，如圖2所示。那麼，空載電流(I0)滯後於電壓V1一個角度ϕ0。其中，ϕ0為空載功率因數角，其大小約為60°-80°，因為為了在機器的氣隙中產生每極所需的磁通量，需要較大的勵磁電流。
現在，在空載狀態下，滑差s = 0，則
$$\mathrm{\frac{𝑅_2}{𝑠}= ∞ \:即\: 空載時開路}$$
$$\mathrm{\therefore 𝐼_0 =\frac{𝑉_1}{𝑍_{𝑁𝐿}}… (2)}$$
其中，
$$\mathrm{𝑍_{𝑁𝐿} = (𝑅_0 \:||\: 𝑗𝑋_0) = 空載阻抗}$$
這裡，所有旋轉損耗都由R0考慮在內。則空載損耗由下式給出：
$$\mathrm{𝑃_0 = 𝑉_1𝐼_0 cos \varphi_0 … (3)}$$
折算到定子側的轉子電流由下式給出：
$$\mathrm{𝐼′_2 =\frac{𝑉_1}{𝑍′_{𝑒1}}=\frac{𝑉_1}{\sqrt{(𝑅_1 +\frac{𝑅′_2}{𝑠})^2+ (𝑋_1 + 𝑋′_2)^2}}… (4)}$$
該轉子電流I′2滯後於電壓V1一個阻抗角ϕ。
參考圖3，
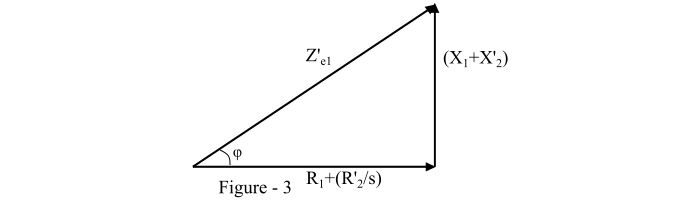
$$\mathrm{sin\:\varphi =\frac{𝑋_1 + 𝑋′_2}{\sqrt{(𝑅_1 +\frac{𝑅′_2}{𝑠})^2+ (𝑋_1 + 𝑋′_2)^2}}… (5)}$$
因此，結合公式(4)和(5)，我們得到：
$$\mathrm{𝐼′_2 =\frac{𝑉_1}{𝑋_1 + 𝑋′_2}sin \varphi; … (6)}$$
公式(6)的形式為𝑟 = 𝑎 sin θ，它表示一個直徑為a的圓。因此，電流(𝐼′2)的軌跡是一個圓，其直徑為
$$\mathrm{直徑 =\frac{𝑉_1}{𝑋_1 + 𝑋′_2}}$$
如圖4所示。
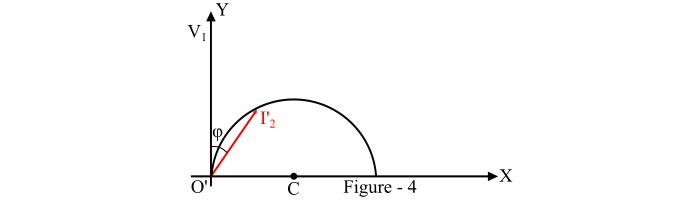
圓的半徑是：
$$\mathrm{O′C =\frac{𝑉_1}{2(𝑋_1 + 𝑋′_2)}}$$
從公式(1)可以看出，定子電流I1是透過組合圖2、圖3和圖4所示的結果得到的。然後，得到的結果如圖5所示，這被稱為感應電動機的圓圖。
感應電動機圓圖的繪製
繪製感應電動機圓圖所需的資料為：
- 定子相電壓，
$$\mathrm{𝑉_1 =\frac{𝑉_𝐿}{\sqrt{3}}}$$
- 電動機的空載電流 (I0)
- 空載功率因數 (cos ϕ0)
- 每相定子電阻 (R1)
- 堵轉電流和功率因數。
繪製感應電動機圓圖的步驟如下：
- 步驟1 – 將定子電壓相量 (V1) 沿y軸取。
- 步驟2 – 選擇一個方便的電流比例尺。以原點O為起點，畫一條長度為I0的線段OO’，該線段與電壓相量V1成ϕ0角。
- 步驟3 – 畫一條垂直於電壓 (V1) 的線段OQN。同樣，畫一條垂直於電壓V1的線段O’D。
- 步驟4 – 從原點O畫一條長度等於堵轉電流 (I1BR) 的線段（與I0使用相同的比例尺）。這條線段滯後於電壓相量V1一個等於堵轉功率因數角(&varphi_{1BR})的角度。
- 步驟5 – 連線O’A並測量其大小（安培）。線段O’A的大小是電流 (I’2BR) 的值。
- 步驟6 – 從點A畫一條平行於電壓相量V1的線段AMN。這條線段垂直於O’D和ON。
- 步驟7 – 計算MP的值為：
$$\mathrm{MP =\frac{𝐼′_{2𝐵𝑅}^{2}𝑅_1}{𝑉_1}}$$
並找到點P。然後，連線O’P並延長它直到與圓相交於點B。需要注意的是，在點B處滑差s為無窮大。 - 步驟8 – 現在，畫出弦O’A的垂直平分線。該垂直平分線將穿過圓心C。因此，以半徑CD’或CD畫圓，這就是感應電動機的圓圖（參見圖5）。
5K+ 次瀏覽
