計算冪的 k 次方模 m

我們的目標是計算冪的 k 次方模 m，其中底數、k 和 m 作為輸入提供。

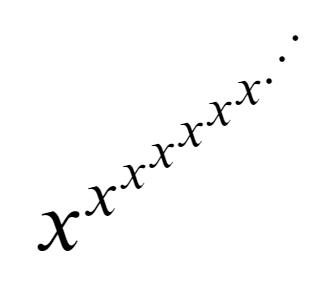
請看上面的圖片。您是否嘗試過計算這樣的問題？讓我們試一試。

計算冪的 k 次方，然後求模 m。

解釋

在這個問題中，給定 x、k 和 m。計算 ${x^{x{^x{^{^.{^{^.{^{^.}}}}}}}}}$ 直到 k 次，然後求模 m。

讓我們用一個例子來理解。

給定，x = 2，k = 4，m = 6

所以，計算 $2^{2^{2{^2}}}\:=\:4^{2{^2}}\:=\:16^2\:=\:256$

然後 256 % 6 = 4。

所以，最終結果是 4。

方法

讓我們討論一下計算冪的 k 次方模 m 的分步演算法。

• 將 x、k 和 m 的值作為輸入。

• 使用 pow 函式計算冪的冪，最後使用模運算子得到最終結果。

• 列印最終結果作為輸出。

計算冪的 k 次方模 m 的 C++ 程式。

#include <iostream>
#include <cmath>
using namespace std;

int powofpow(int x, int k){
   int val = x;
   k--;
   while (k--)
      val = pow(val, x);
 
   return val;
}

int main(){
   int x = 5, k = 2, m = 3;
   int result;
   
   result =  powofpow(x, k);
   result %= m;
   
   cout << "Compute power of power " << k << " times % " << m << " of " << x << " is " << result << endl;
   
   return 0;
}

輸出

Compute power of power 2 times % 3 of 5 is 2

複雜度

時間複雜度：O(k)，因為這段程式碼執行了 (k-1) 次迭代。

空間複雜度：O(1)，因為程式碼使用固定數量的變數來儲存輸入值和結果，與輸入的大小無關。

結論

在本文中，我們試圖解釋計算冪的 k 次方模 m 的方法，其中底數、k 和 m 的值作為輸入給出。我希望本文能幫助您更好地理解這個概念。

Simran Kumari

更新於： 2023年3月23日

120 次瀏覽

開啟您的 職業生涯

透過完成課程獲得認證

開始學習