圖著色

圖著色是一種簡單的方法，用於在某些約束條件下標記圖的元件，例如頂點、邊和區域。在一個圖中，沒有兩個相鄰的頂點、相鄰的邊或相鄰的區域使用最少數量的顏色進行著色。這個數字稱為**色數**，該圖稱為**正確著色圖**。

在圖著色中，對圖設定的約束包括顏色、著色順序、顏色分配方式等。顏色賦予頂點或特定區域。因此，具有相同顏色的頂點或區域構成獨立集。

頂點著色

頂點著色是將顏色分配給圖“G”的頂點，使得任何兩個相鄰頂點都不具有相同的顏色。簡單地說，一條邊的兩個頂點不應具有相同的顏色。

色數

圖“G”頂點著色所需的最少顏色數稱為G的色數，記為X(G)。

當且僅當'GX'是空圖時，χ(G) = 1。如果'GX'不是空圖，則χ(G) ≥ 2

示例

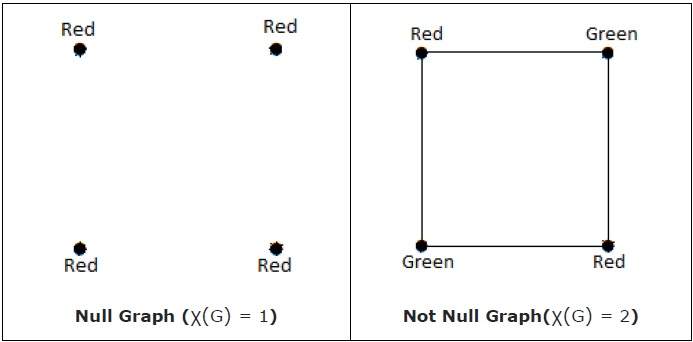
注意 - 如果存在一個最多使用n種顏色的頂點著色，則稱圖“G”為n可覆蓋的，即X(G) ≤ n。

區域著色

區域著色是將顏色分配給平面圖的區域，使得任何兩個相鄰區域都不具有相同的顏色。如果兩個區域具有公共邊，則稱它們為相鄰區域。

示例

看一下下面的圖。區域“aeb”和“befc”是相鄰的，因為這兩個區域之間存在公共邊“be”。

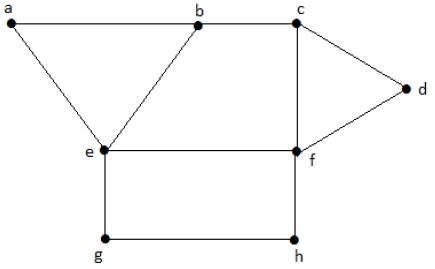
類似地，其他區域也根據鄰接關係進行著色。該圖的著色如下：

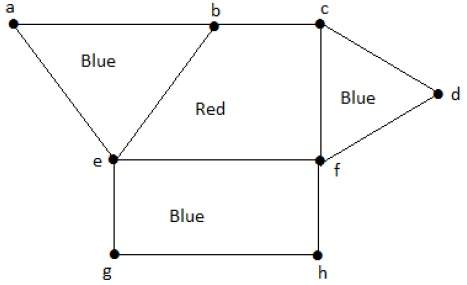
示例

K_n的色數是

a) n

b) n–1

c) ⌊ n / 2 ⌋

d) ⌈ n / 2 ⌉

考慮這個 K₄ 的例子。

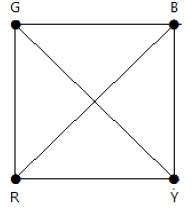
在完全圖中，每個頂點都與其餘 (n – 1) 個頂點相鄰。因此，每個頂點都需要一種新的顏色。因此，K_n 的色數 = n。

圖著色的應用

圖著色是圖論中最重要的概念之一。它用於計算機科學的許多即時應用中，例如：

• 聚類
• 資料探勘
• 影像捕捉
• 影像分割
• 網路
• 資源分配
• 程序排程

Mahesh Parahar

更新於：2019年8月23日

670 次瀏覽

開啟你的職業生涯

透過完成課程獲得認證

開始