資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 中的二項堆?
二項堆被定義為二叉堆的擴充套件，它提供了更快的合併或聯合操作以及二叉堆提供的其他操作。
二項堆被視為二項樹的集合。
什麼是二項樹？
k 階二項樹可以透過取兩棵 k-1 階二項樹並將其中一棵作為另一棵的最左孩子來構建。
k 階二項樹具有以下屬性。
二項樹的節點數正好為 2k。
二項樹的深度為 k。
在深度 i 處正好有 kCi 個節點，其中 i = 0, 1, . . . , k。
根節點的度數為 k，根節點的孩子本身被視為從左到右的 k-1、k-2、...0 階二項樹。
二項堆 -
二項堆被定義為一組二項樹，其中每個二項樹都遵循最小堆屬性。並且對於任何度數，最多隻能有一棵該度數的二項樹。
二項堆示例 -
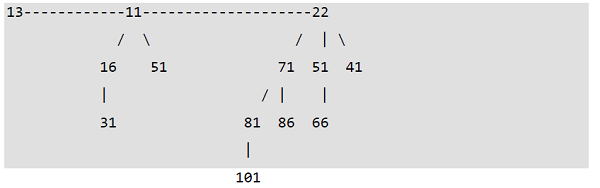
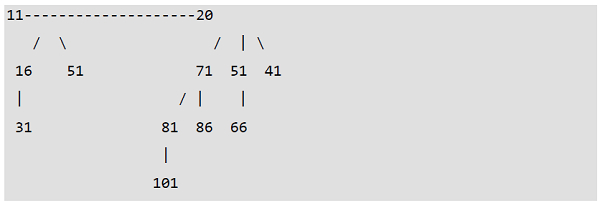
一個擁有 12 個節點的二項堆。它被視為 2 的集合
從左到右的 2 階和 3 階二項樹
二項堆和數字的二進位制表示
一個擁有 m 個節點的二項堆，其二項樹的數量等於 m 的二進位制表示中設定位的數量。例如，假設 m 為 13，m 的二進位制表示（00001101）中有 3 個設定位，這表示 3 棵二項樹。我們還可以將這些二項樹的度數與設定位的位位置相關聯。藉助這種關係，我們可以確定或得出結論，在具有 'm' 個節點的二項堆中，有 O(logm) 棵二項樹。
二項堆的操作 -
union() 是二項堆中的主要操作，所有其他操作主要實現此操作。union() 操作負責將兩個二項堆合併成一個。
insert(h, K) - 將鍵 'K' 插入到二項堆 'h' 中。首先，此操作能夠建立一個具有單個鍵 'K' 的二項堆，然後對 h 和新的二項堆呼叫 union。
getMin(h) - 獲取最小值 getMin() 的一種簡單方法是訪問二項樹根節點的列表並返回最小的鍵。
此應用程式需要 O(logm) 時間。可以透過維護指向最小鍵根節點的指標將其改進為 O(1)。
extractMin(h) - 此操作也實現了 union()。首先，我們呼叫 getMin() 來計算最小鍵二項樹，接下來我們刪除該節點並透過組合已刪除最小節點的所有子樹來建立一個新的二項堆。最後，我們對 h 以及新建立的二項堆呼叫 union()。此操作需要 O(logm) 時間。
delete(h) - 與二叉堆相同，首先，刪除操作將鍵減少到負無窮大，接下來呼叫 extractMin()。
decreaseKey(h) - decreaseKey() 也與二叉堆相同。首先，我們將減小的鍵與其父節點進行比較，如果父節點的鍵更大，則交換鍵並對其父節點進行遞迴。最後，當我們到達父節點具有較小鍵的節點或到達根節點時停止。decreaseKey() 的時間複雜度為 O(logm)。
383 次檢視
