資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究無線通道噪聲：噪聲功率的解題
在本節中，我們將根據白噪聲模型解決一些關於無線通道噪聲的問題。
例題 1
一個白噪聲的雙邊功率譜密度為 6 kW/MHz。它透過一個頻寬為 1 kHz 的低通濾波器。計算輸出噪聲功率。
解答 -
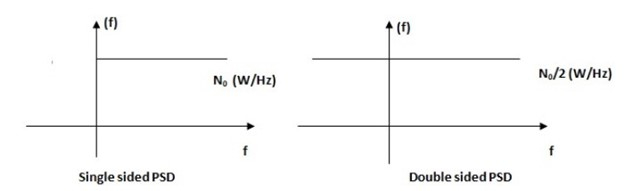
雙邊功率譜密度為 6 kW/MHz。功率譜密度通常以 W/Hz 表示。
$$\frac{6kW}{MHz}=\frac{6000W}{1000000Hz}=\frac{0.006W}{Hz}=\frac{N_{0}}{2}$$
雙邊功率譜密度 N0/2 為 0.006W/Hz。因此，N0 = 0.012W/Hz。
噪聲功率表示為噪聲功率譜密度和噪聲頻寬的乘積。
$$N_{p}=N_{0}.BW$$
$$N_{p}=\frac{0.012W}{Hz}.1kHz=12W$$
該系統的噪聲功率為 12W
例題 2
一個複合電視訊號的頻寬為 40 MHz，並以 0.1 W 的功率透過衛星通道傳輸。白噪聲的雙邊功率譜密度為 10-15 W/Hz。該鏈路的噪聲功率是多少？
解答 - 噪聲功率表示為系統頻寬和噪聲功率譜密度的乘積。噪聲將存在於訊號傳輸的頻率範圍內。因此，訊號頻寬等於噪聲頻寬。
可以使用給定資料找到噪聲的單邊功率譜密度。
$$\frac{N_{0}}{2}=10^{-15}\frac{W}{Hz}\Rightarrow\:N_{0}=2\times\:10^{-15}W/Hz$$
使用給定的值，我們發現噪聲功率為
$$(40\times\:10^{6}).(2\times\:10^{-15})W=80nW$$
例題 3
通訊接收機輸出端可用的噪聲電平為 -10 dBm。絕對尺度上的噪聲電平是多少？
解答 - 絕對尺度上的噪聲功率計算如下：
$$10log_{10}(\frac{N_{p}}{1mW})=-10dBm$$
$$log_{10}(\frac{N_{p}}{1mW})=-1\Rightarrow\:\frac{N_{p}}{1mW}=10^{-1}$$
$$N_{p}=10^{-1}mW=100\mu\:W$$
因此，噪聲功率為 100 微瓦
949 次瀏覽
