資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究在計算機體系結構中，二進位制數的除法是什麼？
二進位制除法類似於十進位制除法。該過程涉及連續比較、移位和減法。與十進位制數的除法相比，二進位制數的除法比較容易，因為商要麼是 0 要麼是 1。也沒有必要檢查被除數（部分餘數）在除數中能容納多少次。
除法溢位
在計算機系統中，除法運算可能導致商溢位，因為暫存器無法容納超過標準長度的數字。為了更好地理解這一點，請考慮一個具有標準 5 位暫存器的系統。
一個暫存器用於儲存除數，另一個暫存器用於儲存被除數。如果商包含 6 位，則商的 5 位將儲存在 5 位暫存器中。因此，溢位位需要一個觸發器來儲存第六位。
如果被除數的高位一半包含一個大於或等於除數的數字，則會發生除法溢位條件。在除法中需要考慮的另一點是，建議避免除以零。當觸發器被置位時，通常會檢測到溢位條件。這個觸發器稱為 DVF。
硬體演算法
藉助圖表可以輕鬆解釋硬體除法演算法。該圖顯示了使用流程圖的硬體除法演算法。
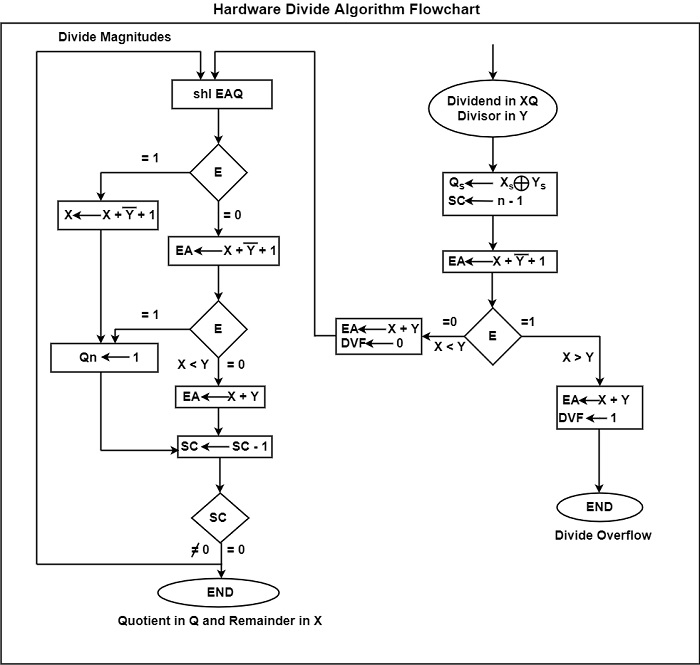
被除數在 X 和 Q 中，除數在 Y 中。結果的符號儲存在 中，它是商的一部分。一個常數被設定為 SC 以確定商中的多位。
除法溢位條件的測試是透過從儲存在 X 中的被除數的一半位中減去存在於 Y 中的除數來進行的。
- 在 XY 的情況下，DVF 被置位，並且操作會過早取消。
- 如果 X < Y，則不會發生除法溢位。因此，透過將 Y 加到 X 來恢復被除數的值。
幅值的除法從將存在於 XQ 中的被除數向左轉移以及將高位轉移到 E 開始。如果轉移到 E 中的位是 1，則 EA > Y，因為 EA 包含一個 1 後跟 n - 1 位，而 Y 只包含 n - 1 位。
因此，從 EA 中減去 Y，並在 QS 中放置 1 作為商位。因為暫存器 X 沒有被除數的高位，所以它的值為 EA - 2n−1。如果將 Y 的 2 的補碼新增到此值，則輸出將如下所示：-
(EA - 2n−1) + ( 22n−1 − Y) = EA − Y
如果 E 應該保持為 1，則來自加法的進位不應該轉移到 E。
如果左移操作將 0 插入 E，則透過插入其 2 的補碼值來減去除數。進位必須轉移到 E。如果 E = 1，則表示 X Y，因此 QS 被設定為 1。如果 E = 0，則表示 X < Y，因此透過將 Y 加到 X 來恢復原始數字。在這種情況下，在移位期間插入的 0 保留在 QS 中。
3K+ 瀏覽量
