計算機體系結構中的定點表示法是什麼？

定點是一種定義階乘數的基本且簡單的方法。定點數使用恆定數量的位。“定點”定義了數字的小數點。沒有自由符號來命名小數點的位置。但是，在二進位制中，位可以是 0 或 1。

十進位制定點表示

定點表示法具有稱為小數點的基數點。小數點位於數字右端 的定點數被視為整數，因為小數點位於數字左端的定點數被視為分數。在這種方法中，小數點的位置是固定的，因為儲存在記憶體中的數字被視為整數或分數。

無符號二進位制數始終被視為正整數，其 MSB 中定義為 0。註冊的二進位制數與負數對比，並在 MSB 中定義為 1。

帶符號二進位制數的大小可以使用三種方法描述，如下所示：

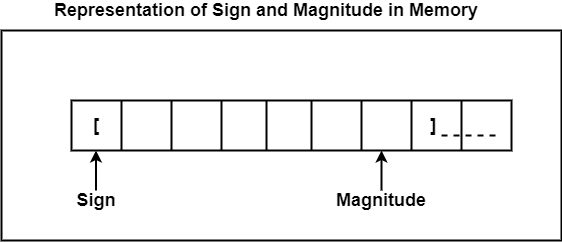
符號和大小表示

在這種方法中，數字中最左邊的位用於表示符號；0 表示正整數，1 表示負整數。數字中其餘的位表示數字的大小。

示例：-24₁₀ 定義為：

10011000

在這個例子中，最左邊的位 1 表示負數，大小為 24。

正值和負值的幅度相等，但它們僅在符號上有所不同。

符號和大小表示法的取值範圍是 -127 到 127。

帶符號的一補數表示

在這種表示法中，負值是透過取等效正數的一補數獲得的。它可以新增帶符號的一補數方法在算術運算過程中產生無法丟棄的進位。

帶符號的一補數表示法的取值範圍是 -127 到 128。

示例：考慮 8 位數的一補數。

(29)₁₀ = (00011101)₂ = 000011101 正值的一補數

-(29)₁₀ = -(00011101)₂ = 111100010 負值的一補數

帶符號的二補數表示

在帶符號的二補數表示法中，一個數的二補數是首先建立該數的一補數，然後將結果加 1 得到的。

帶符號的二補數表示法的取值範圍是 -128 到 127。

示例：考慮 8 位數的二補數。

(29)₁₀= (00011100)₂ = (000011100)₂ 正值的一補數

-(29)₁₀ = -(00011100)₂ = (11110010)₂ 負值的一補數

Ginni

更新於：2021年7月24日

13K+ 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習