資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學靜態互連拓撲的設計空間是什麼？
在靜態網路中，輸入和輸出節點之間的連線是固定的，無法修改。靜態互連網路無法重新配置。這種網路的例子包括線性陣列、環形、弦形環、樹形、星形、胖樹形、網格、環遊、 systolic arrays 和超立方體。靜態互連拓撲的設計空間如圖所示。
線性陣列
這是最基本的互連設計。在這個設計中，處理器連線在一個線性的一維陣列中。第一個和最後一個處理器連線到一個相鄰的處理器，中間的處理元件連線到兩個相鄰的處理器。它是一個一維互連網路。
環形
這是一個簡單的線性陣列，其中端節點連線在一起。它類似於具有環繞連線的網格。環形中的資料傳輸通常是單向的。
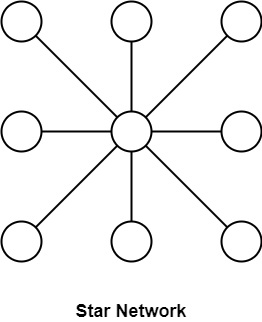
星形
星形連線是另一種簡單且低成本 (C=N-1) 的拓撲結構，如圖所示，它與線性陣列具有相同的較差的二分寬度 (B=1) 和弧連線性 (A=1) 引數，但直徑得到了顯著改善 (D=2)。
樹形互連網路
在樹形互連網路中，處理器按完整的二叉樹方案組織。
胖樹形
它是樹形網路的改進版本。在這個網路中，邊緣的頻寬朝著根部提高。這是對普通樹木的更合理的模擬，其中樹枝向根部加深。
二維網格
這是一個二維網路。在這個網路中，所有處理元件都組織在一個二維網格中。第 i 行第 j 列的處理器用 **PEi,j** 表示。
角上的處理器可以連線到兩個最近的鄰居，即 **PE0,0** 可以連線到 **PE0,1** 和 **PE1,0**。邊界上的處理器可以連線到 3 個相鄰的處理單元，即 **PE0,1** 可以與 **PE0,0、PE0,2** 和 **PE1,1** 互動，內部的處理器可以連線到 4 個相鄰的處理器，即 **PE1,1** 可以連線到 **PE0,1、PE1,0、PE1,2** 和 **PE2,1**。
三維立方體
這是一個三維互連網路。在這個網路中，PE 按立方體結構組織。
超立方體
超立方體互連網路是立方體網路的擴充套件。對於 n ≥ 3，超立方體互連網路可以遞迴地表示如下：
對於 n = 3，它是立方體網路，其中節點被賦予 0、1…7 的二進位制編號。換句話說，其中一個節點被賦予標籤 000，另一個被賦予標籤 001……最後一個節點是 111。
因此，如果任何兩個節點的標籤只在一個位置不同，則任何節點都可以與任何其他節點連線，例如，標籤為 101 的節點可以直接連線到 001、000 和 111。
完全連線網路
從網路直徑 (D=1) 的角度來看，這種拓撲結構是理想的，因為任何兩個節點都是直接連線的。成本 (C=N(N-1)/2) 和節點度 (d=N-1) 引數在構建基於這種拓撲結構的大規模平行計算機時是難以承受的。
瀏覽量 1K+
