樹或連通無環圖

樹是圖，它們不包含任何迴圈。它們以圖形形式表示分層結構。樹屬於最簡單的圖類。儘管它們很簡單，但它們具有豐富的結構。

樹提供了一系列有用的應用，從簡單的家譜到計算機科學資料結構中的複雜樹。

樹

一個**連通無環圖**稱為樹。換句話說，一個沒有迴圈的連通圖稱為樹。

樹的邊稱為**分支**。樹的元素稱為它們的**節點**。沒有子節點的節點稱為**葉子節點**。

具有'n'個頂點的樹具有'n-1'條邊。如果它比'n-1'多一條邊，那麼這條額外的邊顯然必須與兩個頂點配對，從而形成一個迴圈。然後，它成為一個迴圈圖，這違反了樹圖的規則。

示例 1

此處顯示的圖是一個樹，因為它沒有迴圈並且是連通的。它有四個頂點和三條邊，即對於'n'個頂點'n-1'條邊，如定義中所述。

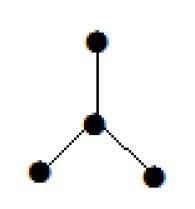
**注意** - 每棵樹至少有兩個度數為一的頂點。

示例 2

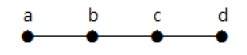
在上面的示例中，頂點'a'和'd'的度數為一。另外兩個頂點'b'和'c'的度數為二。這是可能的，因為為了不形成迴圈，圖中任何地方都應該至少有兩個單邊。它只不過是兩個度數為一的邊。

森林

一個**非連通無環圖**稱為森林。換句話說，樹的互不相連的集合稱為森林。

示例

下面的圖看起來像兩個子圖；但它是一個單個非連通圖。此圖中沒有迴圈。因此，它顯然是一個森林。

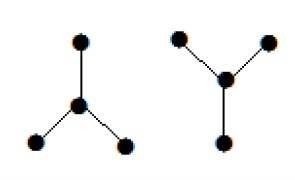
生成樹

設 G 為一個連通圖，則 G 的子圖 H 稱為 G 的生成樹，如果 -

• H 是一棵樹
• H 包含 G 的所有頂點。

無向圖 G 的生成樹 T 是包含 G 所有頂點的子圖。

示例

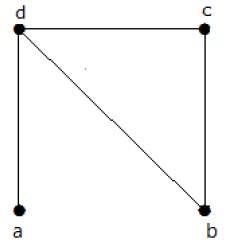
在上面的示例中，G 是一個連通圖，H 是 G 的子圖。

顯然，圖 H 沒有迴圈，它是一棵具有六條邊的樹，比頂點總數少一條。因此，H 是 G 的生成樹。

Mahesh Parahar

更新於： 2019年8月23日

2K+ 瀏覽量

開啟你的 職業生涯

透過完成課程獲得認證

開始學習