一輛汽車的速度-時間圖如圖 8.12 所示。

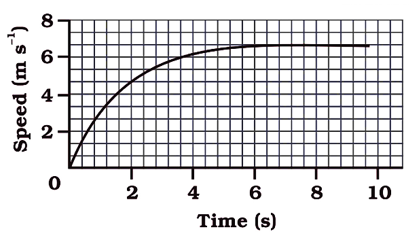
圖 8.12
(a). 求出這輛汽車在最初 4 秒內行駛了多遠。在圖上陰影區域表示汽車在此期間行駛的距離。
(b). 圖的哪個部分表示汽車的勻速運動？

(a) 在速度-時間圖中

距離 = v-t 圖的面積。

這裡，我們使用三角形的面積（天藍色陰影區域）來找到近似面積。

距離 = △OAB 的面積

= $\frac{1}{2}\times b\times h$，其中 b = 底，h = 高

= $\frac{1}{2}\times 4\times 6$ $[\because b=時間,\ h=速度]$

= $12m$

我們仍然沒有得到總面積，因為黃色陰影部分沒有計算在內。所以，這不是精確的。

因此，為了找到黃色區域和天藍色區域的面積，我們需要透過計算方格來找到面積。

從圖中可以看出：

水平軸上的方格數 (時間軸)

5 個方格 = 2 個單位。

$1\ 個方格=\frac{2}{5}個單位$

垂直軸上的方格數 (速度軸)

3 個方格 = 2 個單位。

$1\ 個方格=\frac{2}{3}個單位$

$\therefore 每個方格的面積=\frac{2}{5}\times \frac{2}{3}\Leftrightarrow \frac{4}{15}平方單位$

所以，1 個方格代表 $\frac{4}{15}m$ 距離。

現在，我們取

$\therefore 總面積=15.2+0.8+0.4+0\Leftrightarrow 16.4平方單位$

因此，汽車在 0-4 秒內行駛的距離 = 16.4m

(b) 時間為 t = 6 s 到 10 s 之間綠色部分的圖表示汽車的勻速運動，因為在此時間段內，汽車的速度保持恆定。

教程點

更新於：2022年10月10日

177 次檢視

完成課程獲得認證

開始

一輛汽車的速度-時間圖如圖 8.12 所示。圖 8.12(a). 求出這輛汽車在最初 4 秒內行駛了多遠。在圖上陰影區域表示汽車在此期間行駛的距離。(b). 圖的哪個部分表示汽車的勻速運動？