下表顯示了一年內住院患者的年齡

年齡（歲）	5-15	15-25	25-35	35-45	45-55	55-65
學生人數	6	11	21	23	14	5

求出上述資料的眾數和平均數。比較並解釋這兩個集中趨勢的度量。

已知

一年內住院患者的年齡。

要求

我們需要求出上述資料的眾數和平均數。此外，我們還需要比較並解釋這兩個集中趨勢的度量。

解答

給定資料的頻數如下所示。

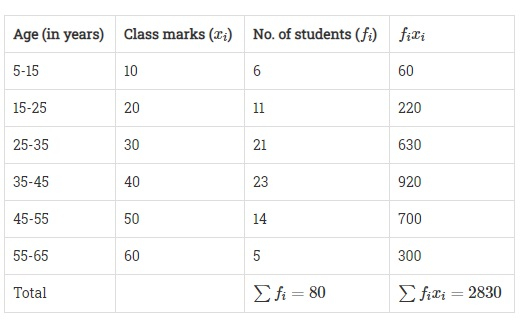
我們觀察到，35-45 的區間具有最大頻數（23）。

因此，它是眾數類。

這裡，

$l=35, h=10, f=23, f_1=21, f_2=14$

我們知道，

眾數 $=l+\frac{f-f_1}{2 f-f_1-f_2} \times h$

$=35+\frac{23-21}{2 \times 23-21-14} \times 10$

$=35+\frac{2}{46-35} \times 10$

$=35+\frac{20}{11}$

$=35+1.81$

$=36.8$

給定資料的眾數為 36.8 歲。

我們知道，

平均數 $=\frac{\sum{f_ix_i}}{\sum{f_i}}$

$=\frac{2830}{80}$

$=35.37$

給定資料的平均數為 35.37 歲。

因此，我們觀察到，在給定資料中，平均數小於眾數。 

教程點

更新於： 2022-10-10

78 次瀏覽

開啟您的 職業生涯

完成課程後獲得認證

開始學習