資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學奇異值分解
機器學習使用奇異值分解的數學方法來理解龐大而複雜的資料集。
在這種數學方法中，一個唯一值矩陣 A 透過分解分解成三個矩陣。就 A 的組成部分而言，矩陣 A 的奇異值分解可以寫成 A=UDVT。在這種情況下，S 表示 A 的奇異值，而 U 和 V 分別代表 A 的左奇異向量和右奇異向量。
數學演算法
給定矩陣 A，求矩陣 A 的轉置 (AT)。
求 A*AT
求 A*AT 的特徵向量
使用公式 A*AT - λ I = 0 求特徵向量，其中 I 是與 A 等價階的單位矩陣。
計算 A 的奇異值，方法是取 ATA 的特徵值的平方根。奇異值按降序排列。
我們計算 A 的左奇異向量和右奇異向量 −
對於每個奇異值，找到 AT A 的相應特徵向量。
每個特徵向量的長度都歸一化為單位長度。
A 的左奇異向量是對應於 A 的非零奇異值的 A AT 的特徵向量。
A 的右奇異向量是 AT A 的歸一化特徵向量。
A 的奇異值（按降序排列）由 S 的對角線元素表示。
A 的左奇異向量由 U 的列表示
V 的列表示 A 的右奇異向量。
示例 1
以下示例對資料集執行 SVD 並將其繪製為散點圖。資料集從 UCI 資料集載入，資料根據引數進行分離。資料經過標準化處理，並將 .svd() 應用於資料（這是 Numpy 的 linalg（線性代數）模組的一部分）。使用散點圖繪製資料。
演算法
步驟 1 − 匯入 Pandas、Numpy 和 Matplotlib 庫。
步驟 2 − 將資料集的連結儲存在 url 變數中。
步驟 3 − 將特徵（即資料集的列名）儲存在名為 names 的陣列中。
步驟 4 − 使用 pd.read_csv() 方法讀取資料
步驟 5 − 特徵與目標分離
步驟 6 − 使用公式 (X - Xmean) / 標準差 X 標準化特徵
步驟 7 − 使用 Numpy 的 linalg 模組的 .svd() 方法對 X 執行 SVD
步驟 8 − 構造對角矩陣 S
步驟 9 − 使用 Matplotlib 的 .scatter() 方法繪製 U
步驟 10 − 執行程式碼後，可以在彈出視窗中看到散點圖
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
url='https://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data'
names = ['Length', 'Diam', 'Height', 'Whole']
abalone = pd.read_csv(url, names=names)
X = abalone.iloc[:, :-1].values
y = abalone.iloc[:, -1].values
X = (X - X.mean(axis=0)) / X.std(axis=0)
U, s, Vt = np.linalg.svd(X, full_matrices=False)
S = np.diag(s)
plt.scatter(U[:, 0], U[:, 1], c=y)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
輸出
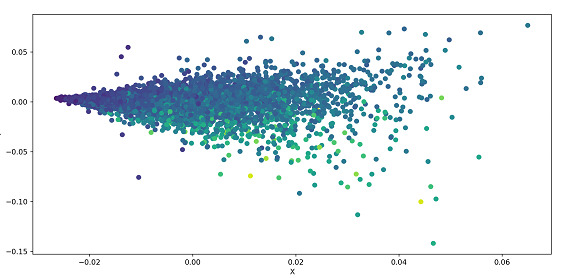
示例 2
在以下示例中，我們計算矩陣 A 的 SVD，該矩陣作為引數傳遞給函式。我們計算特徵向量和特徵值，並按降序排列它們。該函式返回特徵向量、奇異值和右奇異矩陣的轉置。
演算法
步驟 1 − 匯入 numpy 庫
步驟 2 − 定義一個函式 svd，它接受矩陣 A 作為輸入
步驟 3 − 使用 Numpy 的 linalg 方法的 .eigh() 方法計算 A^T * A 的特徵值和特徵向量。
步驟 4 − 特徵向量和特徵值按降序排列。
步驟 5 − 計算 A 的奇異值和右奇異向量
步驟 6 − 該函式返回特徵向量、奇異值和右奇異矩陣的轉置。
步驟 7 − 將值儲存在陣列 A 中，並使用 A 作為引數呼叫函式 svd
步驟 8 − 將函式返回的值分別儲存在 U、S、V 中並列印它們
import numpy as np def svd(A): eigen_values, eigen_vectors = np.linalg.eigh(np.dot(A.T, A)) sorted_indices = eigen_values.argsort()[::-1] eigen_values = eigen_values[sorted_indices] eigen_vectors = eigen_vectors[:,sorted_indices] singular_values = np.sqrt(eigen_values) right_singular_vectors = np.dot(A, eigen_vectors) right_singular_vectors /= singular_values return eigen_vectors, singular_values, right_singular_vectors.T A = np.array([[1, 2, 2], [4, 5, 9], [7, 8, 10]]) U, S, V = svd(A) print (U) print (S) print (V)
在上述程式碼中，svd() 函式以矩陣作為輸入，並計算矩陣的特徵值和特徵向量。我們將計算出的特徵值和特徵向量按降序排列，並透過取特徵值的平方根來計算奇異值並將它們儲存在陣列中。
然後，我們透過將矩陣與排序後的特徵向量相乘並將結果除以之前計算的奇異值來計算右奇異向量。因此，該函式返回特徵向量、奇異值和右奇異向量的轉置。
輸出
[[-0.43649583 -0.55427262 -0.70869828] [-0.52004753 -0.48734746 0.70145778] [-0.73418115 0.67474019 -0.07552297]] [18.45494908 1.76319494 0.5531709 ] [[-0.15957525 -0.59354546 -0.7888216 ] [-0.10179655 0.80469488 -0.58489624] [ 0.98192322 -0.01303565 -0.18883027]]
結論
奇異值分解有助於減少包含大量值的資料集。此外，此方法有助於為較小的值生成有意義的解決方案。但是，這些較小的值也包含原始資料中巨大的變異性。SVD 用於影像壓縮中的低秩近似、推薦系統中的低秩近似、主成分分析和線性迴歸。
瀏覽量 329 次
