資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究R → L
解決方案
步驟 1 - 首先，將其轉換為增強文法 G' 並對產生式進行編號
(0) S′ → S
(1) S → L = R
(2) S → R
(3) L →∗ R
(4) L → id
(5) R → L
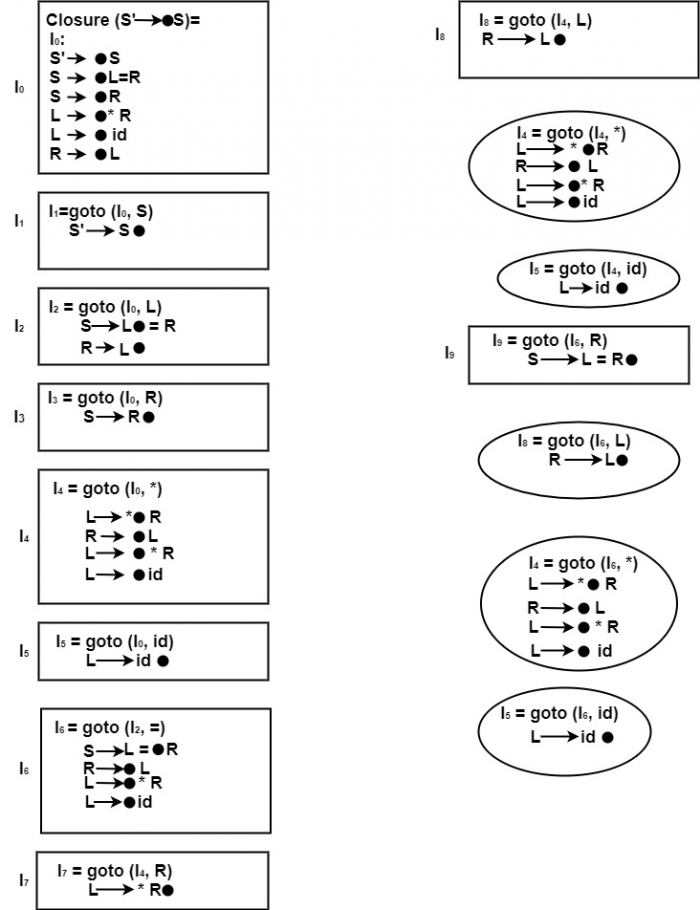
步驟 2 - 查詢閉包和 goto 函式以構造 LR(0) 專案。
在以下 LR(0) 專案集中，方框表示新狀態，圓圈表示重複狀態
步驟 3 - FOLLOW 的計算 - 應用 FOLLOW 的規則 (1)，我們得到
FOLLOW(S) = $ (1)
- S → L = R
應用規則 (2) FOLLOW - 將 S → L = R 與 A → α B β 進行比較。
| S → | Ε | L | = R |
| A → | Α | B | Β |
∴ A = S，α = ε，B = L，β = {= R}
FIRST(β) = FIRST(= R) = {=} 不包含 ε
規則 (2a) of FOLLOW
FOLLOW(L) = {=} (2)
應用規則 (3) of FOLLOW - 將 S → L = R 與 A → α B 進行比較
| S → | L = | R |
| A → | α | Β |
∴ FOLLOW(R) = {FOLLOW(S)} (3)
- S → R
規則 (2) of FOLLOW 無法應用。
由於 S → R 無法與 A → α B β 進行比較。因為，如果我們比較，我們會得到，α = ε，B = R，β = ε。但 β 不應為 ε 以應用此規則。
應用規則 (3) of FOLLOW - 將 S → R 與 A → α B 進行比較
| S → | ε | R |
| A → | α | Β |
∴ A = S，α = ε，B = R
FOLLOW(R) = {FOLLOW(S)} (4)
- L →*R
規則 (2) of FOLLOW 無法應用。
由於 L →* R 無法與 A → α B β 進行比較。因為 β 將為 ε，這是不可能的。
應用規則 (3) of FOLLOW - 將 L →∗ R 與 A → α B 進行比較
| L → | * | R |
| A → | α | Β |
∴ A = L，α =∗，B = R
FOLLOW(R) = {FOLLOW(L)} (5)
- L →id
規則 (2) 和 (3) of FOLLOW 無法應用。
由於 L → id 無法與 A → α B β 和 A → α B 匹配。
- R → L
規則 (2) 無法應用。
由於 R → L 無法與 A → α B β 匹配。
應用規則 (3) of FOLLOW - 將 R → L 與 A → α B 進行比較
| R → | E | L |
| A → | A | Β |
∴ A = R，α = ε，B = L
FOLLOW(L) = {FOLLOW(R)} (6)
結合語句 (1) 到 (6)
FOLLOW(S) = $ (1)
FOLLOW(L) = {=} (2)
FOLLOW(R) = {FOLLOW(S)} (3)
FOLLOW(R) = {FOLLOW(S)} (4)
FOLLOW(R) = {FOLLOW(L)} (5)
FOLLOW(L) = {FOLLOW(R)} (6)
從 (1)
FOLLOW(S) = $
從 (1)、(2)、(3)、(4)、(5)、(6)。
FOLLOW(L) = FOLLOW(R) = {=, $}
構造解析表
填充移進項 (s)
由於 goto (I0,*) = I4
∴ Action [0,∗] = s4
由於 goto (I0, id) = I5
∴ Action [0, id] = s5
類似地，所有移進項 (s) 都填充到表中。
填充歸約項 (r)
應用規則 (2b) SLR 解析表的構造
考慮
I2 S → L ∙= R
R → L ∙
R → L ∙ 與 A → α ∙ 進行比較
| R → | L | . |
| A → | α | . |
∴ A = R，α = L
由於 R → L 是給定問題中的產生式編號 (5)。
∴ 在第 2 行狀態和第 = 列、$ 列前面寫入 r5。
類似地，歸約的其他條目填充到表中。
填充“接受”條目
考慮 I1
I1 - S′ → S ∙
應用解析表構造規則 (4)
∴ 在第 1 行狀態和第 $ 列前面寫入“接受”。
透過填充所有移進、歸約、goto 和接受條目，我們得到以下解析表。
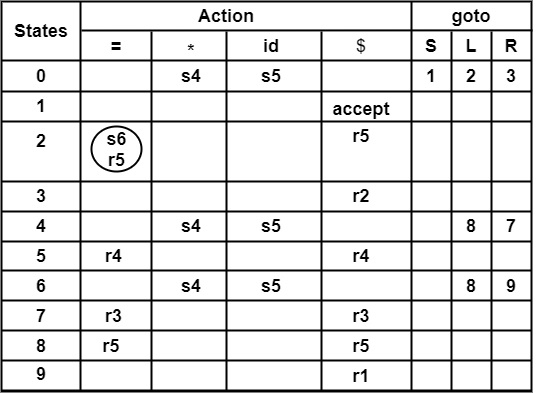
下表精確地顯示 Action [2, =] = s6 或 r5 中有多個條目。
狀態 I2 - S → L ∙ = R
R → L ∙
R → L ∙ 具有 A → α ∙ 的形式
∴ 可以對其應用歸約規則。
R → L 是給定問題中的產生式編號 (5)。
∴ Action [2, =] = r5
∴ goto (I2, =) = I6
∴ Action [2, =] = s6
因此，在條目 Action [2, =] 上存在移進/歸約衝突。這表明給定的文法不是 SLR(1) 文法。
3K+ 次檢視
