三維空間中的截距公式

---

簡介

截距公式可以應用於位於二維或三維空間中的線段。線段的分割是一種方法或過程，其中線段被分成幾個部分（相等或不相等）。點用於分割線段。它是一種重要的座標幾何方法，用於確定三角形的重心、內心和外心。在本教程中，我們將討論三維幾何、截距公式和距離公式，並提供一些例題。

三維座標幾何

三維座標幾何表示三維空間中的幾何圖形。它需要三個座標來表示三維平面中任何點的位置。此外，這三個座標告訴我們點在 X 軸、Y 軸和 Z 軸上的位置。三條軸的交點稱為原點（如圖所示）。在現實生活中，我們看到各種物體，它們具有高度、深度和寬度。這些被稱為三維幾何。

三維幾何中的截距公式

截距公式根據點相對於線段的相對位置進行分類。在座標幾何中存在兩種型別的截距公式，例如：

• 內分公式

• 外分公式

現在，我們將詳細討論每種截距公式。

內分公式

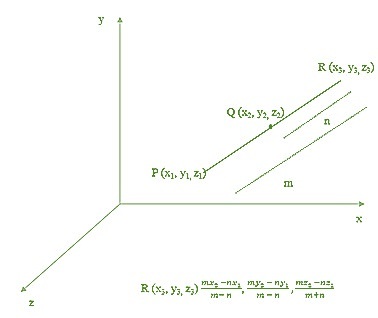
在這種型別的分割中，線段被一個點在內部分割成兩部分。例如，考慮一條線段，其端點的座標為

$\mathrm{P(x_{1}y_{1}z_{1})\:和\:Q(x_{2}y_{2}z_{2}).\:一個點\:R(x_{3}y_{3}z_{3})}$被線段在 m:n 的比例下內分（如圖所示）。現在，可以使用以下公式確定點 $\mathrm{R(x_{3}y_{3}z_{3})}$ 的座標。

$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{mx_{2}\:+\:nx_{1}}{m\:+\:n}\:,\:\frac{my_{2}\:+\:ny_{1}}{m\:+\:n}\:,\:\frac{mz_{2}\:+\:nz_{1}}{m\:+\:n})}$

如果我們分開座標，我們將得到

x 軸座標 $\mathrm{=\:\frac{mx_{2}\:+\:nx_{1}}{m\:+\:n}}$ , y 軸座標 $\mathrm{=\:\frac{my_{2}\:+\:ny_{1}}{m\:+\:n}}$ z 軸座標 $\mathrm{\frac{mz_{2}\:+\:nx_{1}}{m\:+\:n}}$

外分公式

在這種型別的分割中，線段被一個點在外部分割成兩部分。例如，考慮一條線段，其端點的座標為 $\mathrm{P(x_{1},y_{1}z_{1})\:和\:Q(x_{2},y_{2},z_{2})\:.\:一個點\:R(x_{3},y_{3},z_{3})}$ 被線段在 m:n 的比例下外分（如圖所示）。現在，可以使用以下公式確定點 $\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})}$ 的座標。

$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{mx_{2}\:-\:nx_{1}}{m\:-\:n}\:,\:\frac{my_{2}\:-\:ny_{1}}{m\:-\:n}\:,\:\frac{mz_{2}\:-\:nz_{1}}{m\:-\:n})}$

如果我們分開座標，我們將得到

x 軸座標 $\mathrm{=\:\frac{mx_{2}\:-\:nx_{1}}{m\:-\:n}}$ , y 軸座標 $\mathrm{=\:\frac{my_{2}\:-\:ny_{1}}{m\:-\:n}}$ z 軸座標 $\mathrm{\frac{mz_{2}\:-\:nx_{1}}{m\:-\:n}}$

三維幾何中的距離公式（簡述）

讓我們考慮線段端點的座標為 $\mathrm{P(x_{1},y_{1},z_{1})\:和\:Q(x_{2},y_{2},z_{2})}$ 透過點 P 和 Q，我們繪製平行於直角座標系的平面，使得 $\mathrm{\angle\:QPR\:=\:90°\:和\:\angle\:PSR\:=\:90°}$

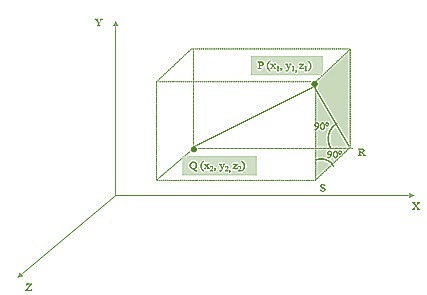
在三角形 PQR 中使用勾股定理，

$\mathrm{PQ^{2}\:=\:PR^{2}\:+\:QR^{2}..................(1)}$

類似地，在三角形 PSR 中使用勾股定理，

$\mathrm{PR^{2}\:=\:PS^{2}\:+\:RS^{2}..................(2)}$

將 $\mathrm{PR^{2}}$ 的值代入公式 (1)，得到

$\mathrm{PQ^{2}\:=\:PS^{2}\:+\:RS^{2}\:+\:QR^{2}.................(3)}$

使用點的座標，$\mathrm{PS\:=\:y_{2}\:-\:y_{1}\:,\:RS\:=\:z_{2}\:-\:z_{1}\:,\:QR\:=\:x_{2}\:-\:x_{1}}$

現在，將 PS、RS 和 QR 的值代入公式 (3)

$$\mathrm{\Longrightarrow\:PQ^{2}\:=\:(y_{2}\:-\:y_{1})^{2}\:+\:(z_{2}\:-\:z_{1})^{2}\:+\:(x_{2}\:-\:x_{1})^{2}}$$

$$\mathrm{\Longrightarrow\:PQ\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}\:+\:(z_{2}\:-\:z_{1})^{2}}}$$

例題

例 1

考慮線段端點的座標為 (-1, -3, 2), (0, 11, 5)。求出將上述線段在 2:1 的比例下內分的點的座標。

解答 -

根據題目，

線段端點的座標 $\mathrm{=\:(-1\:,\:-3\:,\:2)\:,\:(0\:,11\:,\:5)}$

與標準座標進行比較，$\mathrm{x_{1}\:=\:-1\:,\:y_{1}\:=\:-3\:,\:z_{1}\:=\:2\:,\:x_{2}\:=\:0\:,\:y_{2}\:.\:z_{2}\:=\:5}$

內分比例 = 2:1 (這裡，m= 2, n=1)

假設 $\mathrm{R(x_{3},y_{3},z_{3})}$ 為所求點。

使用內分公式，

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{mx_{2}\:+\:nx_{1}}{m\:+\:n}\:,\:\frac{my_{2}\:+\:ny_{1}}{m\:+\:n}\:,\:\frac{mz_{2}\:+\:nz_{1}}{m\:+\:n})}$$

$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{2\:\times\:(0)\:+\:1\:\times\:(-1)}{2\:+\:1}\:,\:\frac{2\:\times\:(0)\:+\:1\:\times\:(-1)}{2\:+\:1}\:,\:\frac{2\:\times\:5\:+\:1\:\times\:2}{2\:+\:1})}$

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{-1}{3},\frac{19}{3},4)}$$

∴所求點的座標為 $\mathrm{(\frac{-1}{3},\frac{19}{3},4)}$

例 2

線段端點的座標為 (1, -4, -9) 和 (8, -3, -1)。求出將上述線段在 3:5 的比例下外分的點的座標。

解答 -

已知，

線段端點的座標 = (1, -4, -9) 和 (8, -3, -1)

與標準座標進行比較，$\mathrm{x_{1}\:=\:1,y_{1}\:=\:-4,z_{1}\:=\:-9,x_{2}\:=\:8,y_{2}\:=\:-3,z_{2}\:=\:-1}$

外分比例 $\mathrm{=\:3\colon\:5\:(m\:=\:3\:,\:n\:=\:5)}$

使用外分公式，

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{mx_{2}\:-\:nx_{1}}{m\:-\:n}\:,\:\frac{my_{2}\:-\:ny_{1}}{m\:-\:n}\:,\:\frac{mz_{2}\:-\:nz_{1}}{m\:-\:n})}$$

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{3\:\times\:-\:5\:\times\:1}{3\:-\:5},\frac{3\:\times\:(-3)\:-\:(-4)}{3\:-\:5},\frac{3\:\times\:(-1)\:-\:5\:\times\:(-9)}{3\:-\:5})}$$

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{-19}{2},\frac{-11}{2},21)}$$

∴所求點的座標為 $\mathrm{(\frac{-19}{2},\frac{-11}{2},21)}$

例 3

檢查給定點是否共線。$\mathrm{P(-1,0,7)\:,Q(3,2,1)\:,\:R(5,3,-2)}$

解答 -

如果給定點共線，則兩條線段距離之和將等於第三條線段的距離。

現在，使用三維距離公式

$\mathrm{PQ\:=\:\sqrt{(3\:-\:(-1))^{2}\:+\:(2\:-\:0)^{2}\:+\:(1\:-\:7)^{2}}}$

$$\mathrm{\Longrightarrow\:PQ=\:\sqrt{16\:+\:4\:36}\:=\:\sqrt{}56}\:=\:2\sqrt{}14$$

$\mathrm{QR\:=\:\sqrt{(5\:-\:3)^{2}\:+\:(3\:-\:2)^{2}\:+\:(-2\:-\:1)^{2}}}$

$$\mathrm{\Longrightarrow\:QR=\:\sqrt{4\:+\:1\:+\:9}\:=\:\sqrt{14}}$$

$\mathrm{PR\:=\:\sqrt{(5\:-\:(-1))^{2}\:+\:(3\:-\:0)^{2}\:+\:(-2\:-\:7)^{2}}}$

$$\mathrm{\Longrightarrow\:QR\:=\:\sqrt{36\:+\:9\:+\:81}\:=\:\sqrt{126}\:=\:3\sqrt{14}}$$

由於 $\mathrm{PQ\:+\:QR\:=\:PR}$ ，因此給定的三個點共線。

應用題

問題 1：線段端點的座標為 (8, 0, -1) 和 (- 2, -7, -5)。求出將上述線段在 7:10 的比例下外分和內分的點的座標。

問題 2：求出 z 軸上與點 (10, 2, 1) 和 (-5, -7, 2) 等距的點的座標。

結論

本教程簡要介紹了使用截距公式在三維幾何中分割線段。此外，還簡要描述了確定兩點之間距離的公式。此外，還提供了一些例題，以便更好地理解這個概念。總之，本教程可能有助於理解三維空間中的截距公式。

常見問題

1. 如果一個點是線段的中點，那麼分割比例是多少？

如果點是線段的中點，它必須將線段分成兩等分。在這種情況下，比例，即 m: n，將為 1:1。

2. 比例 m: n 可以為負數嗎？

可以。在外分中，比例 m: n 為負值。

3. 截距公式可以應用於二維幾何嗎？

可以。在二維座標幾何中，每個點在 x 和 y 方向上都有兩個座標。

4. 截距公式和中點公式有什麼區別？

在截距公式中，點以任意比例分割線段，即 m: n。但是，在中點公式的情況下，點以 1:1 的比例分割線段。

5. 兩點之間的距離可以為負數嗎？

不可以。兩點之間的距離始終為正整數。