標量三重積

---

介紹

標量三重積用於求平行六面體的體積，平行六面體是平行四邊形的 3 維形式。由於它是一個三重積，因此它處理從一個公共頂點開始的三個相鄰邊的三個向量。

$\mathrm{平行六面體體積\:=\:\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$

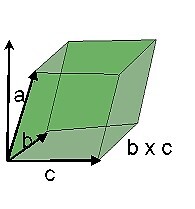
我們知道平行六面體底面的面積是平行四邊形的面積 $\mathrm{=\:l\:\times\:b}$

$\mathrm{底面積\:=\:\lvert\:\overrightarrow{b}\:\times\:\overrightarrow{c}\:\rvert}$

要找到平行六面體的高度，b × c 是畫到 b 和 c 的一條垂直線，它不是平行六面體的實際高度。我們首先考慮長方體的高度，並將其轉換為平行六面體。$\mathrm{\overrightarrow{a}\:在\:\overrightarrow{b}\:\times\:\overrightarrow{c}上的投影}$給出平行六面體的高度。

$\mathrm{\overrightarrow{a}\:.\:\frac{(\overrightarrow{b}\:\times\:\overrightarrow{c})}{\:\lvert\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:\rvert}}$

現在求平行六面體的體積

$\mathrm{底面積\:\times\:高度\:=\mathrm{\overrightarrow{a}\:.\:\frac{(\overrightarrow{b}\:\times\:\overrightarrow{c})}{\:\lvert\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:\rvert}\:\:\lvert\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:\rvert}}$

$\mathrm{平行六面體體積\:=\:\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$

向量

許多向量是位移向量，表示物體移動的距離和方向。向量既包含大小也包含方向。大小表示多少，方向表示角度。向量越長，幅度越大。如果一個向量連線兩個向量 A 和 B，我們可以將其寫成 $\mathrm{\overrightarrow{AB}}$

標量積或點積

兩個向量的乘積稱為標量積或點積。當兩個向量 $\mathrm{\overrightarrow{A}\:和\:\overrightarrow{B}}$ 相乘時，我們使用 (•) 表示它，即 $\mathrm{\overrightarrow{A}\:.\:\overrightarrow{B}}$。這可以理解為 $\mathrm{\overrightarrow{A}\:和\:\overrightarrow{B}}$ 的點積。點積只能用於在相同維度上相乘兩個向量。

例如

考慮兩個向量 $\mathrm{A\:=\:(p,q,r)\:和\:B\:=\:(u,v,w)}$

解決方案

要找到 A 和 B 的點積，將 A 的 x 分量乘以 B 的 x 分量

$\mathrm{A\:.\:B\:=\:(pu)\:+\:(qv)\:+\:(rw)}$

點積的結果始終只是一個數字。

當角度 𝛳 位於 $\mathrm{\overrightarrow{a}\:和\:\overrightarrow{b}}$ 之間時，要找到點積，

$\mathrm{a\:.\:b\:=\:\lvert\:a\:\rvert\:\lvert\:b\:\rvert\:\cos\:\theta}$

$\mathrm{\cos\:\theta\:=\:\frac{a\:.\:b}{\lvert\:a\:\rvert\:\lvert\:b\:\rvert}}$

其中 $\mathrm{\lvert\:a\:\rvert\:\:和\:\lvert\:b\:\rvert\:}$ 是大小。

向量積或叉積

設向量 A 和向量 B 為兩個向量，向量積或叉積的結果是垂直線。叉積用符號 (×) 表示，即 $\mathrm{A\:\times\:B}$。在叉積中，乘法的順序很重要，這意味著 $\mathrm{A\:\times\:B\neq\:B\:\times\:A}$

例如

如果 $\mathrm{\overrightarrow{A}\:=\:x_{1}\widehat{i}\:+\:y_{1}\widehat{j}\:+\:z_{1}\widehat{k}\:和\:\overrightarrow{B}\:=\:x_{2}\widehat{i}\:+\:y_{2}\widehat{j}\:+\:z_{2}\widehat{k}}$ 計算 $\mathrm{\overrightarrow{A}\:\times\:\overrightarrow{B}}$

解決方案

給定 $\mathrm{\overrightarrow{A}\:=\:x_{1}\widehat{i}\:+\:y_{1}\widehat{j}\:+\:z_{1}\widehat{k}}$

$\mathrm{\overrightarrow{B}\:=\:x_{2}\widehat{i}\:+\:y_{2}\widehat{j}\:+\:z_{2}\widehat{k}}$

要找到叉積，使用行列式

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{vmatrix} \widehat{i} & \widehat{j} & \widehat{k} \\ x_{1} & y_{1} & z_{1}\\ x_{2} & y_{2} & z_{2}\end{vmatrix}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\widehat{i}\:(y_{1}z_{2}\:-\:y_{2}z_{1})\:-\:\widehat{j}\:(x_{1}z_{2}\:-\:x_{2}z_{1})\:\widehat{k}\:(x_{1}y_{2}\:-\:x_{2}y_{1})}$

標量三重積

考慮三個向量 $\mathrm{\overrightarrow{A}\:=\:x_{1}\widehat{i}\:+\:x_{2}\widehat{j}\:+\:x_{3}\widehat{k}\:,\:\overrightarrow{B}\:=\:y_{1}\widehat{i}\:+\:y_{2}\widehat{j}\:+\:y_{3}\widehat{k}\:,\:\overrightarrow{C}\:=z_{1}\widehat{i}\:+\:z_{2}\widehat{j}\:+\:z_{3}\widehat{k}}$ 求標量三重積

解決方案

要找到標量三重積，

$\mathrm{\widehat{a}\:.\:(\widehat{b}\:\times\:\widehat{c})}$

$\mathrm{\widehat{B}\:\times\:\widehat{C}\:=}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{vmatrix} \widehat{i} & \widehat{j} & \widehat{k} \\ y_{1} & y_{2} & y_{3}\\ z_{2} & z_{2} & z_{3}\end{vmatrix}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\widehat{i}\:(y_{2}z_{3}\:-\:y_{3}z_{2})\:-\:\widehat{j}\:(y_{1}z_{3}\:-\:y_{3}z_{1})\:\widehat{k}\:(y_{1}z_{2}\:-\:y_{2}z_{1})}$

現在

$\mathrm{\widehat{a}\:.\:(\widehat{b}\:\times\:\widehat{c})}$

$\mathrm{(x_{1}\widehat{a}\:+\:x_{2}\widehat{j})\:.\:(\widehat{i}(y_{2}z_{3}\:-\:y_{3}z_{2})\:\:-\:\widehat{j}(y_{1}z_{3}\:-\:y_{3}z_{1})\:+\:\widehat{k}(y_{1}z_{2}\:-\:y_{2}z_{1})}$

$\mathrm{(x_{1}(y_{2}z_{3}\:-\:y_{3}z{2})\:+\:x_{2}(y_{1}z_{3}\:-\:y_{3}z_{1})\:+\:x_{2}(y_{1}z_{2}\:-\:y_{2}z_{1}))}$

標量三重積是 $\mathrm{\widehat{a}\:.\:(\widehat{b}\:\times\:\widehat{c})\:=}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{vmatrix} x_{1} & x_{2} & x_{3} \\ y_{1} & y_{2} & y_{3}\\ z_{2} & z_{2} & z_{3} \end{vmatrix}}$

三個向量的共面性

向量 A、B、C 位於同一平面上，平行六面體的體積為零。

如果 $\mathrm{\widehat{a}\:.\:(\widehat{b}\:\times\:\widehat{c})\:=\:0}$ 則三個向量共面。

解題示例

1. 如果 $\mathrm{A\:=\:4\widehat{i}\:+\:3\widehat{j}}$ 和 $\mathrm{B\:=\:3\widehat{i}\:+\:11\widehat{j}}$，求 A 和 B 的點積

解決方案

$\mathrm{(\overrightarrow{A}\:.\:\overrightarrow{B})\:=\:(4\:\times\:3)\:+\:(3\:\times\:11)}$

$\mathrm{=\:45}$

2. 求 $\mathrm{u\:=\:\widehat{i}\:+\:2\widehat{j}\:和\:v\:=\:2\widehat{i}\:+\:\widehat{j}}$ 之間的夾角

解決方案

$\mathrm{\cos\:\theta\:=\:\frac{u\:.\:v}{\lvert\:u\:\rvert\:\lvert\:v\:\rvert\:}}$

$\mathrm{u\:.\:v\:=\:2(1)\:+\:(2)1\:+\:4}$

$\mathrm{\lvert\:u\:\rvert\:=\:\sqrt{(1^{2})\:+\:(2^{2})}\:=\:\sqrt{1\:+\:4}\:=\:\sqrt{5}}$

$\mathrm{\lvert\:v\:\rvert\:=\:\sqrt{(2^{2})\:+\:(1^{2})}\:=\:\sqrt{4\:+\:1}\:=\:\sqrt{5}}$

$\mathrm{\cos\:\theta\:=\:\frac{4}{\sqrt{5}\:.\:\sqrt{5}}}$

$\mathrm{\theta\:=\:\cos^{-1}(\frac{4}{5})}$

3. 求 $\mathrm{A\:=\:3\widehat{i}\:+\:2\widehat{j}\:-\:5\widehat{k}}$ 和 $\mathrm{2\widehat{i}\:-\:6\widehat{j}\:+\:9\widehat{k}}$ 的叉積

解決方案

$$\mathrm{\begin{vmatrix} \widehat{i} & \widehat{j} & \widehat{k} \\ 3 & 2 & -1\\ 2 & -6 & 9 \end{vmatrix}}$$

$\mathrm{\widehat{i}((2)(9)\:-\:(-5)(-6))\:-\:\widehat{j}(3)(9)\:-\:(2)(-5)\:+\:\widehat{k}((3)(-6)\:-\:(2)(2))}$

$\mathrm{=\:\widehat{i}(18\:-\:30)\:-\:\widehat{j}(27\:+\:10)\:+\:\widehat{k}(-18\:-\:4)}$

$\mathrm{=\:-(1\widehat{i}\:+\:37\widehat{j}\:+\:22\widehat{k})}$

4. 檢查給定的向量是否共面，如果

$\mathrm{A\:=\:2\widehat{i}\:+\:\widehat{j}\:+\:3\widehat{k}\:,\:B\:=\:\widehat{i}\:+\:3\widehat{j}\:+\:\widehat{k}\:,\:C\:=\:2\widehat{i}\:+\:2\widehat{j}\:+\:\widehat{k}}$ 求 $\mathrm{\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$

解決方案

$\mathrm{\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$

$$\mathrm{\begin{vmatrix} 2 & 1 & 3 \\ 1 & 3 & 1\\ 2 & 2 & 1 \end{vmatrix}}$$

$\mathrm{=\:2(3\:-\:2)\:-1(1\:-\:2)\:+\:3(2\:-\:6)}$

$\mathrm{=\:2(1)\:-\:1(-1)\:+\:3(-4)}$

$\mathrm{=\mathrm{2\:+\:1\:-12\:=\:-9}}$

標量三重積不共面。

求標量三重積，如果 $\mathrm{A\:=\widehat{i}\:+\:2\widehat{j}\:+\:\widehat{k}\:;\:B\:=\:2\widehat{i}\:+\:\widehat{j}\:+\:3\widehat{k}\:;\:C\:=\:3\widehat{i}\:+\:3\widehat{j}\:\widehat{k}}$

解決方案

$\mathrm{\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})}$

$$\mathrm{\begin{vmatrix} 1 & 2 & 1 \\ 2 & 1 & 3\\ 3 & 3 & 1 \end{vmatrix}}$$

$\mathrm{=\:-8\:-\:14\:+\:3\:=\:19}$

結論

標量三重積是用於求平行六面體體積的三維測量。叉積以矩陣形式表示，透過取行列式。點積是直接相乘，它還可以測量向量之間的夾角。

常見問題

1. 迴圈排列會影響標量三重積嗎？

不會，三個向量 a、b 和 c 的迴圈排列不會影響標量積，它保持不變。

$\mathrm{[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]\:=\:[\overrightarrow{b},\overrightarrow{a},\overrightarrow{c}]\:=\:[\overrightarrow{c},\overrightarrow{a},\overrightarrow{b}]}$

2. 當點積和叉積互換時，標量三重積會發生什麼？

當點積和叉積互換時，標量三重積的值保持不變

即，$\mathrm{\overrightarrow{a}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:=\:(\overrightarrow{a}\:\times\:\overrightarrow{b})\:.\:\overrightarrow{c}}$

3. 如果任何兩個值改變其位置，標量三重積會發生什麼變化？

當任何兩個向量的順序發生變化時，它將變為負數

即，$\mathrm{[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]\:=\:-\:[\overrightarrow{b},\overrightarrow{a},\overrightarrow{c}]}$

4. 當標量三重積中重複兩個向量時會發生什麼？

當兩個向量重複時，標量三重積將為零，即，

$\mathrm{[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]\:,\:[\overrightarrow{b},\overrightarrow{b},\overrightarrow{c}]\:,\:[\overrightarrow{a},\overrightarrow{c},\overrightarrow{c}]}$

即，$\mathrm{[\overrightarrow{a},\overrightarrow{a},\overrightarrow{c}]\:=\:\overrightarrow{a}\:.\:(\overrightarrow{a}\:\times\:\overrightarrow{c})\:=\:0}$

$\mathrm{[\overrightarrow{b},\overrightarrow{b},\overrightarrow{c}]\:=\:\overrightarrow{b}\:.\:(\overrightarrow{b}\:\times\:\overrightarrow{c})\:=\:0}$

5. 當標量三重積中的所有向量都相同時會發生什麼？

當所有三個向量都相同時，標量三重積將為零，即 $\mathrm{[\overrightarrow{a},\overrightarrow{a},\overrightarrow{a}]}$

即，$\mathrm{[\overrightarrow{a},\overrightarrow{a},\overrightarrow{a}]\:=\:\overrightarrow{a}\:.\:(\overrightarrow{a}\:\times\:\overrightarrow{a})\:=\:0}$