資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 中無符號整數的恢復除法演算法
討論使用除法演算法對無符號整數進行除法。一些除法演算法應用於紙上，另一些則在數位電路中實現。除法演算法分為兩種型別：慢速除法演算法和快速除法演算法。慢速除法演算法包括恢復、非恢復、SRT 和非恢復演算法。
在本教程中，我們將討論恢復演算法，假設 0 < 除數 < 被除數。
求解方法
在這裡，我們將使用暫存器 Q 儲存商，暫存器 A 儲存餘數，M 儲存除數。A 的初始值保持為 0，並且其值被恢復，這就是這種方法被稱為恢復除法的原因。
用值初始化暫存器，
Q = 被除數，
A = 0，
M = 除數，
N = 被除數的位數。
AQ 左移意味著將暫存器 A 和 Q 作為一個單元。
用 A 減去 M 並存儲在 A 中。
檢查 A 的最高有效位
如果為 0，則將最低有效位設定為 1。
否則，將最低有效位設定為 0。
恢復 A 的值並遞減計數器 N 的值。
如果 N = 0，則退出迴圈；否則，轉到步驟 2。
商儲存在暫存器 Q 中。
流程圖
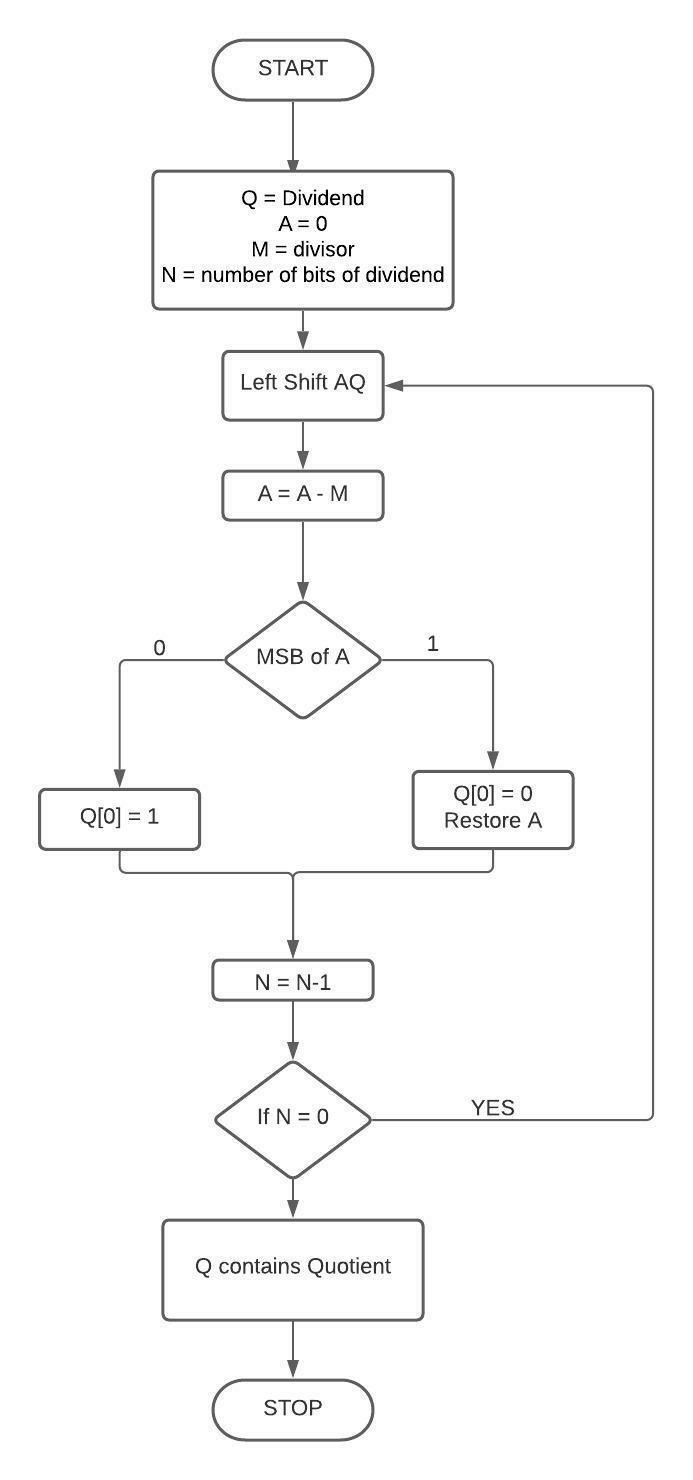
示例
上述方法的 C++ 程式碼
#include <iostream>
using namespace std;
int main(){
// initializing all the variables with Dividend = 9, Divisor = 2.
int Q = 8,q=1,M=3;
short N = 4;
int A = Q;
M <<= N;
// loop for division by bit operation.
for(int i=N-1; i>=0; i--) {
A = (A << 1)- M;
// checking MSB of A.
if(A < 0) {
q &= ~(1 << i); // set i-th bit to 0
A = A + M;
} else {
q |= 1 << i; // set i-th bit to 1
}
}
cout << "Quotient: "<< q;
return 0;
}輸出
Quotient: 2
結論
在本教程中，我們討論了無符號整數的恢復除法演算法。我們討論了一種使用流程圖和應用位運算來解決此問題的簡單方法。我們還討論了此問題的 C++ 程式，我們可以使用 C、Java、Python 等程式語言來完成。希望本教程對您有所幫助。
更新於： 2021 年 11 月 26 日
1K+ 瀏覽量
廣告