反射角

---

簡介

角是兩條相交直線之間旋轉的角度。角可以有多種型別，例如銳角、直角、鈍角等。其中一種角是反射角。反射角是兩條直線之間角度的反射。由於我們無法使用量角器測量大於 180° 的角，因此我們可以藉助反射角來測量角度。在本教程中，我們將學習角、角的型別、反射角、凹多邊形、現實生活中的反射角以及一些關於反射角的解題示例。

角

角定義為二維幾何中兩條直線或射線之間旋轉的角度。角也可以定義為從同一點發出的兩條射線之間形成的角度變化。

角的型別

根據角的大小，可以將角劃分為不同的類別。

• 銳角 - 如果兩條直線相交形成小於 90 度的角，則該角稱為銳角。

• 直角 - 如果兩條直線相交形成 90 度的角，則該角稱為直角。

• 鈍角 - 如果兩條直線相交形成大於 90 度的角，則該角稱為鈍角。

• 平角 - 如果兩條直線相交形成等於 180 度的角，則所成的角稱為平角。

• 反射角 - 如果兩條直線相交形成大於 180 度小於 360 度的角，則該角稱為反射角。

• 周角 - 如果兩條直線相交形成等於 360 度的角，則該角稱為周角。

反射角

反射角是兩條直線之間形成的角度，它是主角的反射。反射角的旋轉角度可以在 180° 到 360° 之間。一個角與其反射角一起構成一個周角。我們知道周角是 360°，對於一個角 x，相應的反射角將是 360-x。

下圖給出了一個反射角。該圖顯示了兩條直線之間的角度及其對應的反射角，兩者結合構成一個周角。反射角有助於我們確定大於 180° 的角度。

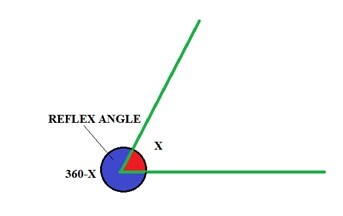
在給定一個角 x 的情況下，要找到反射角，我們可以從 360° 中減去角 x。

假設給定的角為 x，如上圖所示。

我們知道周角為 360°。

因此，反射角 = 360°-x

凹多邊形

有一個或多個內角大於 180° 的多邊形稱為凹多邊形。

凹多邊形至少有四條邊，並且不能是正多邊形。

另一方面，凸多邊形是一個所有角都小於 180° 的多邊形。因此，凹多邊形與凸多邊形相反。

如多邊形圖所示，其中一個角為 260°，大於 180°。

現實生活中的反射角

就像角一樣，我們可以在日常生活中隨處可見反射角。因為我們到處都能看到角，所以一定會有與角相關的反射角。一些例子有 -

• 時鐘 - 模擬時鐘是反射角的最佳例子之一，因為我們每天都在各個地方看到它。假設時鐘敲響 3 點，我們知道時針和分針形成 90° 的角。因此，該角度之間的數字將是 1、2 和 3。而如果我們尋找反射角，則該角度將包括數字 4、5、6、7、8、9、10、11 和 12。

• 比薩 - 如果你看到一個比薩，它是一個圓形。當我們沿著它的中心將比薩切成塊並取出一塊時，空隙形成一個角，而剩下的比薩顯示出它的反射角。

解題示例

1.對於一個角 $\mathrm{\angle AOB== 57^\circ}$，求反射角 $\mathrm{\angle AOB}$ 的值。

解：我們知道一個角及其反射角共同構成一個周角。因此，反射角可以透過以下公式計算

$$\mathrm{\angle AOB = 360^\circ - 57^\circ = 303^\circ.}$$

2.根據反射角的性質判斷真或假。

• 反射角可以是鈍角。

• 170° 是反射角。

• 反射角可以是周角

解

• 否，鈍角小於 180°，而反射角應大於 180°。

• 錯誤，170° 不是反射角，因為它是一個鈍角。

• 反射角不能是周角，因為周角是 360°，而反射角小於 360°。

3.給出反射角的例子。

解

我們知道反射角在 180° 和 360° 之間

因此，如果我們將銳角、直角或鈍角加到平角上，就會得到反射角。

結論

角是兩條相交直線之間旋轉的角度。角可以有多種型別，例如銳角、直角、鈍角等。其中一種角是反射角。反射角是兩條直線之間形成的角度，它是主角的反射。反射角的旋轉角度可以在 180° 到 360° 之間。有一個或多個內角大於 180° 的多邊形稱為凹多邊形。另一方面，凸多邊形是一個所有角都小於 180° 的多邊形。模擬時鐘是反射角的最佳例子之一。當我們沿著它的中心將比薩切成塊時，剩下的比薩顯示出它的反射角。

角的型別	描述
銳角	小於 90° 的角
直角	等於 90° 的角
鈍角	大於 90° 的角
平角	等於 180° 的角
反射角	180° 和 360° 之間的角。
周角	等於 360° 的角。

常見問題

1. 反射角的一些例子是什麼？

200°、225°、270° 和 315° 是一些反射角。

2. 什麼是凸多邊形？

凸多邊形是一個所有內角都小於 180° 的多邊形。

3. 什麼是凹多邊形？

凹多邊形是一個至少有一個角大於 180° 的多邊形。

4. 反射角與主角有什麼區別？

主角不能大於 180°，而反射角總是大於 180°。

5. 求反射角的公式是什麼？

反射角可以透過從 360° 中減去主角來獲得。