資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++程式中樹的祖先-後代關係查詢
在這個問題中，我們給定一個 N 個頂點的樹和 Q 個查詢，每個查詢包含兩個值 i 和 j。我們的任務是建立一個程式來解決樹中祖先-後代關係的查詢。
為了解決每個查詢，我們需要檢查節點 i 是否是樹中節點 j 的祖先。
讓我們舉個例子來理解這個問題，
輸入
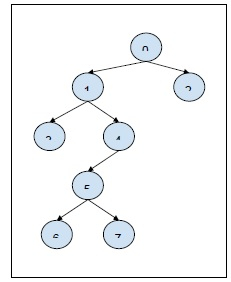
Q = 2, query[][] = {{3, 5}, {1, 6}}輸出
No Yes
解釋
i = 3, j = 5: The node 3 is not the ancestor of node 5. Return NO. i = 1, j = 6: The node 1 is the ancestor of node 6. Return YES.
解決方案方法
解決這個問題的一種方法是使用樹遍歷技術，即深度優先搜尋（DFS）。我們將從第 i 個節點開始遍歷，向下遍歷到其所有後代，然後檢查第 j 個節點是否是其後代。解決這個問題的一個有效方法是找出每個節點的進入時間和退出時間。並檢查它們是否共享祖先-後代關係。
程式說明我們解決方案的工作原理，
示例
#include <bits/stdc++.h>
using namespace std;
void depthFirstSearch(vector<int> g[], int u, int parent, int entTime[], int exitTime[], int& cnt){
entTime[u] = cnt++;
for (int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if (v != parent) depthFirstSearch(g, v, u, entTime, exitTime, cnt);
}
exitTime[u] = cnt++;
}
void calcTimeInAndOut(int edges[][2], int V, int entTime[], int exitTime[]){
vector<int> g[V];
for (int i = 0; i < V - 1; i++) {
int u = edges[i][0];
int v = edges[i][1];
g[u].push_back(v);
g[v].push_back(u);
}
int cnt = 0; depthFirstSearch(g, 0, -1, entTime, exitTime, cnt);
}
int main(){
int edges[][2] = { { 0, 1 }, { 0, 2 }, { 1, 3 }, { 1, 4 }, { 4, 5 }, { 5, 6 }, { 5, 7 }};
int E = sizeof(edges) / sizeof(edges[0]);
int V = E + 1;
int Q = 2;
int query[Q][2] = {{3, 5}, {1, 6}};
int entTime[V], exitTime[V];
calcTimeInAndOut(edges, V, entTime, exitTime);
for(int i = 0; i < Q; i++){
cout<<"For query "<<(i+1)<<" : "; (entTime[query[i][0]] <= entTime[query[i][1]] && exitTime[query[i][0]] <= exitTime[query[i][1]])? cout<<"is Ancestor\n":cout<<"is not Ancestor\n";
}
return 0;
}輸出
For query 1 : is Ancestor For query 2 : is not Ancestor
更新於: 2020年12月22日
196 次檢視
廣告