資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
JavaScript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會科學
時尚研究
法律研究求解 C++ 中棋盤中方格數量的程式
在此問題中，我們將獲得一個棋盤的大小。我們的任務是建立一個程式來用 C++ 求出棋盤中方格的數量。
問題描述 − 求解棋盤中方格的數量。我們需要計算棋盤中所有方格的組合，即認為邊長為 1x1、2x2、3x3 ... nxn 的方格。
讓我們透過一個示例來理解該問題:
輸入: n = 4.
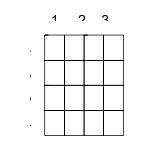
輸出: 30
Squares of size 1x1 -> 16 Squares of size 2x2 -> 9 Squares of size 3x3 -> 4 Squares of size 4x4 -> 1 Total number of squares = 16+9+4+1 = 30
解決方案方法
A simple approach is by using the sum formula for nxn grid. Let’s deduct the general formula for the sum, sum(1) = 1 sum(2) = 1 + 4 = 5 sum(3) = 1 + 4 + 9 = 14 sum(4) = 1 + 4 + 9 + 16 = 30 The sum is can be generalised as sum = 12 + 22 + 32 + 42 + … n2 sum = ( (n*(n+1)*((2*n) + 1))/6 )
示例
#include <iostream>
using namespace std;
int calcSquaresCount(int n){
int squareCount = ( (n * (n+1) * (2*n + 1))/6 );
return squareCount;
}
int main() {
int n = 6;
cout<<"The total number of squares of size "<<n<<"X"<<n<<" is
"<<calcSquaresCount(n);
}輸出
The total number of squares of size 6X6 is 91
更新日期: 01-Oct-2020
瀏覽 2 千次+
廣告