資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學C++實現二叉樹的後序遍歷（無遞迴、無棧）
在本問題中，我們給定一棵二叉樹。我們的任務是不使用遞迴和棧來列印二叉樹的後序遍歷。
二叉樹是一種特殊的樹，其中每個節點最多可以有兩個子節點。
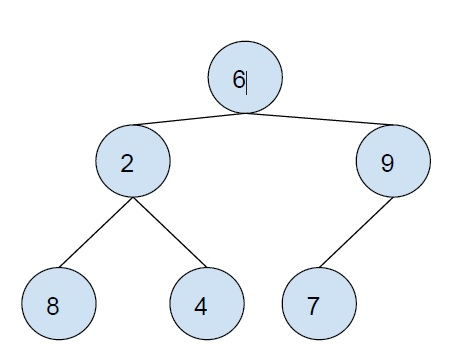
後序遍歷是一種樹遍歷技術，其中首先遍歷左子樹，然後遍歷右子樹，最後遍歷根節點。
上述樹的後序遍歷為：8 4 2 7 9 6
為了在不使用遞迴和棧的情況下遍歷樹，我們將使用基於深度優先搜尋的技術，並將資料儲存在雜湊表中。
示例
展示此解決方案實現的程式：
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
void postOrderTraversal(struct Node* head) {
struct Node* temp = head;
unordered_set<Node*> visited;
while (temp && visited.find(temp) == visited.end()) {
if (temp->left &&
visited.find(temp->left) == visited.end())
temp = temp->left;
else if (temp->right &&
visited.find(temp->right) == visited.end())
temp = temp->right;
else {
cout<<temp->data<<"\t";
visited.insert(temp);
temp = head;
}
}
}
struct Node* insertNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main(){
struct Node* root = insertNode(6);
root->left = insertNode(2);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->right = insertNode(4);
root->right->left = insertNode(7);
root->right->left->left = insertNode(13);
cout<<"Post Order Traversal of the binary tree :\n";
postOrderTraversal(root);
return 0;
}輸出
Post Order Traversal of the binary tree : 8 4 2 13 7 9 6
可以更新相同的解決方案，並消除雜湊表的用法。因為它的作用是儲存已訪問的節點。我們將為樹本身的每個節點新增一個已訪問標誌以減少系統負載，這將使我們的演算法更好。
一個更有效的解決方案是使用無序對映，這將減少回溯到頭的開銷。
示例
展示此解決方案實現的程式：
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
bool visited;
};
void postOrderTraversal(Node* root) {
Node* n = root;
unordered_map<Node*, Node*> postorder;
postorder.insert(pair<Node*, Node*>(root, nullptr));
while (n) {
if (n->left && postorder.find(n->left) == postorder.end()) {
postorder.insert(pair<Node*, Node*>(n->left, n));
n = n->left;
}
else if (n->right && postorder.find(n->right) == postorder.end()) {
postorder.insert(pair<Node*, Node*>(n->right, n));
n = n->right;
}
else {
cout<<n->data<<"\t";
n = (postorder.find(n))->second;
}
}
}
struct Node* insertNode(int data) {
struct Node* node = new Node;
node->data = data;
node->left = NULL;
node->right = NULL;
node->visited = false;
return (node);
}
int main() {
struct Node* root = insertNode(6);
root->left = insertNode(2);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->right = insertNode(4);
root->right->left = insertNode(7);
root->right->left->left = insertNode(13);
cout<<"Post Order Traversal of the binary tree :\n";
postOrderTraversal(root);
return 0;
}輸出
Post Order Traversal of the binary tree : 8 4 2 13 7 9 6
更新於：2020年4月17日
瀏覽量：353
廣告