資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學C++二叉樹中節點的後序遍歷後續節點
在這個問題中，我們給定一個二叉樹和一個節點。我們的任務是列印該二叉樹中節點的後序遍歷後續節點。
二叉樹是一種特殊的樹，其中每個節點最多可以有兩個子節點。
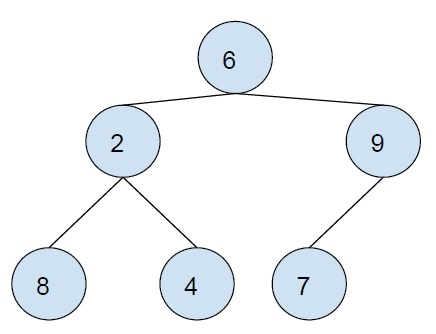
後序遍歷是一種樹遍歷技術，其中首先遍歷左子樹，然後遍歷右子樹，最後遍歷根節點。
上述樹的後序遍歷：8 4 2 7 9 6
讓我們來看一個例子來理解這個問題。
輸入 - 上例中的二叉樹，節點 = 7
輸出 - 9
解釋 - 我們可以在二叉樹的後序遍歷中看到它。
為了解決這個問題，一個簡單、容易且適合初學者的解決方案是簡單地找到後序遍歷，然後列印遍歷中下一個數字。
但是我們需要學習更有效的解決方案，
有效的解決方案將涉及對後序遍歷進行一些一般的觀察。
由於根節點是後序遍歷中的最後一個節點，因此它的後續節點是 NULL。
如果當前節點是右子節點，則父節點是後續節點。
如果當前節點是左子節點，則
如果缺少右兄弟節點，則後續節點是父節點
如果存在右兄弟節點，則該節點或其最左邊的子節點是後續節點。
這種方法是有效的，時間複雜度為 O(h)，h 是樹的高度。
示例
程式演示了我們解決方案的實現，
#include <iostream>
using namespace std;
struct Node {
struct Node *left, *right, *parent;
int value;
};
struct Node* insertNode(int value) {
Node* temp = new Node;
temp->left = temp->right = temp->parent = NULL;
temp->value = value;
return temp;
}
Node* findPostorderSuccessor(Node* root, Node* n) {
if (n == root)
return NULL;
Node* parent = n->parent;
if (parent->right == NULL || parent->right == n)
return parent;
Node* curr = parent->right;
while (curr->left != NULL)
curr = curr->left;
return curr;
}
int main(){
struct Node* root = insertNode(6);
root->parent = NULL;
root->left = insertNode(2);
root->left->parent = root;
root->left->left = insertNode(8);
root->left->left->parent = root->left;
root->left->right = insertNode(4);
root->left->right->parent = root->left;
root->right = insertNode(9);
root->right->parent = root;
root->right->left = insertNode(7);
root->right->left->parent = root->right;
root->left->right->left = insertNode(14);
struct Node* successorNode = findPostorderSuccessor(root, root->left->right);
if (successorNode)
cout<<"Postorder successor of "<<root->left->right->value<<" is "<<successorNode->value;
else
cout<<"Postorder successor of "<<root->left->right->value<<" is NULL";
return 0;
}輸出
Postorder successor of 4 is 2
更新於：2020年4月17日
595 次瀏覽
廣告