資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究牽引電動機的簡單電阻起動
在**簡單電阻起動方法**中，牽引電動機兩端的電壓從零逐漸升高到額定線電壓，並且透過逐漸減小外部電阻將電流保持在額定值。
假設：
𝑇 = 起動時間（秒）
𝑉 = 線電壓（伏）
𝐼 = 恆定電流（安培）
那麼，在接通電源的瞬間，電機產生的反電動勢為零，並且隨著電機開始旋轉，反電動勢立即開始建立。
在任何時刻，電機供電電壓等於電機產生的反電動勢加上電機串勵繞組和電樞上的電壓降加上起動電阻上的電壓降，即：
$$\mathrm{\mathit{V\mathrm{\: =\: }E_{b}\mathrm{\: +\: }I\left ( R_{se} \mathrm{\: +\: }R_{a}\right )\mathrm{\: +\: }IR\mathrm{\: =\: }E_{b}\mathrm{\: +\: }IR_{m}\mathrm{\: +\: }IR}}$$
下圖說明了牽引電動機簡單電阻起動中的電壓降和能量損耗。
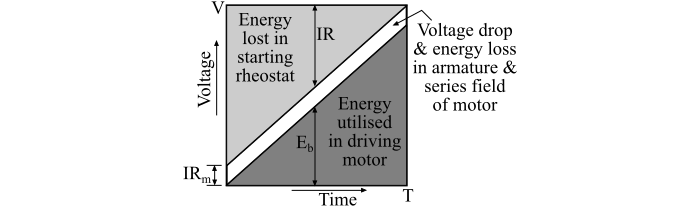
在起動結束時，外部電阻減小到零，因此外部電阻上的電壓降為零，反電動勢近似等於線電壓，因此：
$$\mathrm{\mathit{E_{b}\mathrm{\: =\: }V-IR_{m}}}$$
因此，起動期間從電源汲取的能量為：
$$\mathrm{起動期間能量\mathrm{\: =\: }\mathit{V\times I\times T}}$$
外部電阻上的能量損耗為：
$$\mathrm{外部電阻能量損耗\mathrm{\: =\: }外部電阻平均電壓降\times 電流\times 時間}$$
$$\mathrm{\Rightarrow 外部電阻能量損耗\mathrm{\: =\: }\mathit{\frac{V-IR_{m}\mathrm{\: +\: }\mathrm{0}}{\mathrm{2}}\times I\times T}}$$
如果忽略串勵繞組和電機電樞上的電壓降，則：
$$\mathrm{\therefore 外部電阻能量損耗\mathrm{\: =\: }\frac{1}{2}\mathit{V\times I\times T}}$$
因此，用於驅動電機的能量為：
$$\mathrm{利用能量\mathrm{\: =\: }供給能量\, -\, 外部電阻能量損耗}$$
$$\mathrm{\Rightarrow 利用能量\mathrm{\: =\: }\mathit{VIT-\mathrm{\frac{1}{2}}VIT\mathrm{\: =\: }\mathrm{\frac{1}{2}}VIT}}$$
此外，電機的起動效率為：
$$\mathrm{\eta \mathrm{\: =\: }\frac{利用能量}{供給能量}\times 100\mathrm{\: =\: }\mathit{\frac{VIT/\mathrm{2}}{VIT}}\times 100\mathrm{\: =\: }50\%}$$
586 次瀏覽
