資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 中的完美矩形
假設我們有 N 個軸對齊的矩形，我們需要檢查它們是否共同形成了一個精確的矩形區域的覆蓋。這裡每個矩形都表示為左下角點和右上角點。因此，一個單位正方形表示為 [1,1,2,2]。（左下角點為 (1, 1)，右上角點為 (2, 2)）。
所以，如果輸入像 rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]，那麼輸出將為 true，因為所有 5 個矩形共同形成了一個精確的矩形區域的覆蓋。
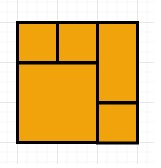
為了解決這個問題，我們將遵循以下步驟：
定義一個集合 visited
area := 0
x2 := -inf, x1 := inf
y2 := -inf, y1 := inf
對於給定列表 re 中的每個 r：
x1 := r[0] 和 x1 的最小值
x2 := r[2] 和 x2 的最大值
y1 := r[1] 和 y1 的最小值
y2 := r[3] 和 y2 的最大值
area := area + ((r[2] - r[0]) * (r[3] - r[1]))
s1 := r[0] 連線 r[1]
s2 := r[0] 連線 r[3]
s3 := r[2] 連線 r[3]
s4 := r[2] 連線 r[1]
如果 s1 已被訪問，則：
從 visited 中刪除 s1
否則
將 s1 插入 visited
如果 s2 已被訪問，則：
從 visited 中刪除 s2
否則
將 s2 插入 visited
如果 s3 已被訪問，則：
從 visited 中刪除 s3
否則
將 s3 插入 visited
如果 s4 已被訪問，則：
從 visited 中刪除 s4
否則
將 s4 插入 visited
s1 := 連線 x1 和 y1
s2 := 連線 x2 和 y1
s3 := 連線 x1 和 y2
s4 := 連線 x2 和 y2
如果 s1、s2、s3、s4 均未被訪問，則
返回 false
當 area 等於 ((x2 - x1) * (y2 - y1)) 時返回 true
示例
讓我們看看以下實現以更好地理解：
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
bool isRectangleCover(vector<vector<int>> &re) {
unordered_set<string> visited;
int area = 0;
int x2 = INT_MIN;
int x1 = INT_MAX;
int y2 = INT_MIN;
int y1 = INT_MAX;
for (auto &r : re) {
x1 = min(r[0], x1);
x2 = max(r[2], x2);
y1 = min(r[1], y1);
y2 = max(r[3], y2);
area += (r[2] - r[0]) * (r[3] - r[1]);
string s1 = to_string(r[0]) + to_string(r[1]);
string s2 = to_string(r[0]) + to_string(r[3]);
string s3 = to_string(r[2]) + to_string(r[3]);
string s4 = to_string(r[2]) + to_string(r[1]);
if (visited.count(s1)) {
visited.erase(s1);
}
else
visited.insert(s1);
if (visited.count(s2)) {
visited.erase(s2);
}
else
visited.insert(s2);
if (visited.count(s3)) {
visited.erase(s3);
}
else
visited.insert(s3);
if (visited.count(s4)) {
visited.erase(s4);
}
else
visited.insert(s4);
}
string s1 = to_string(x1) + to_string(y1);
string s2 = to_string(x2) + to_string(y1);
string s3 = to_string(x1) + to_string(y2);
string s4 = to_string(x2) + to_string(y2);
if (!visited.count(s1) || !visited.count(s2) || !visited.count(s3) || !visited.count(s4) || visited.size() != 4)
return false;
return area == (x2 - x1) * (y2 - y1);
}
};
main() {
Solution ob;
vector<vector<int>> v = {{1, 1, 3, 3}, {3, 1, 4, 2}, {3, 2, 4, 4}, {1, 3, 2, 4}, {2, 3, 3, 4}};
cout << (ob.isRectangleCover(v));
}輸入
{{1, 1, 3, 3}, {3, 1, 4, 2}, {3, 2, 4, 4}, {1, 3, 2, 4}, {2, 3, 3, 4}}輸出
1
177 次檢視
