Python實現尋找最深葉節點的最近公共祖先

假設我們有一個根二叉樹，我們需要返回其最深葉節點的最近公共祖先。需要注意的是：

  • 二叉樹中的節點只有在沒有子節點時才是葉節點。

  • 樹的根節點深度為0，當節點深度為d時，其每個子節點的深度為d+1。

  • 節點集合S在節點A中的最近公共祖先是指深度最大的節點A，使得S中的每個節點都在以A為根的子樹中。

如果輸入是[1,2,3,4,5],

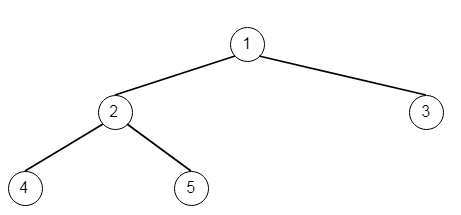
則輸出為[2,4,5]

為了解決這個問題，我們將遵循以下步驟：

  • 定義一個名為solve()的方法，它將接收一個節點作為引數，其工作方式如下：

  • 如果節點不存在，則返回一個列表[0, None]

  • 如果節點的左子樹和右子樹為空，則返回一個列表[1, None]

  • d1, l := solve(節點的左子樹), d2, r := solve(節點的右子樹)

  • 如果d1 > d2，則返回列表[d1 + 1, l]

  • 否則，如果d2 > d1，則返回列表[d2 + 1, r]

  • 返回列表[d1 + 1, 節點]

  • 在主方法中，我們將執行：

  • list := solve(根節點)

  • return list[1]

示例(Python)

讓我們看看下面的實現來更好地理解：

線上演示

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.data = data
      self.left = left
      self.right = right
def insert(temp,data):
   que = []
   que.append(temp)
   while (len(que)):
      temp = que[0]
      que.pop(0)
      if (not temp.left):
         if data is not None:
            temp.left = TreeNode(data)
         else:
            temp.left = TreeNode(0)
         break
      else:
         que.append(temp.left)
      if (not temp.right):
         if data is not None:
            temp.right = TreeNode(data)
         else:
            temp.right = TreeNode(0)
         break
      else:
         que.append(temp.right)
def make_tree(elements):
   Tree = TreeNode(elements[0])
   for element in elements[1:]:
      insert(Tree, element)
   return Tree
def print_tree(root):
   #print using inorder traversal
   if root is not None:
      print_tree(root.left)
      print(root.data, end = ', ')
      print_tree(root.right)
class Solution(object):
   def lcaDeepestLeaves(self, root):
      return self.solve(root)[1]
   def solve(self,node):
      if not node:
         return [0,None]
      if not node.left and not node.right:
         return [1,node]
      d1,l = self.solve(node.left)
      d2,r = self.solve(node.right)
      if d1>d2:
         return [d1+1,l]
      elif d2>d1:
         return [d2+1,r]
      return [d1+1,node]
ob = Solution()
root = make_tree([1,2,3,4,5])
print_tree(ob.lcaDeepestLeaves(root))

輸入

[1,2,3,4,5]

輸出

4, 2, 5,

更新於：2020年4月30日

瀏覽量：119

開啟你的職業生涯

完成課程獲得認證

開始學習
廣告
© . All rights reserved.