廣度優先搜尋 (BFS)

圖是物件集合的一種圖形表示，其中某些物件對透過連結連線。相互連線的物件由稱為頂點的點表示，連線頂點的連結稱為邊。

正式地，圖是一對集合(V, E)，其中V是頂點集，E是連線頂點對的邊集。請看下面的圖 -

在上圖中，

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

廣度優先搜尋 (BFS)

廣度優先搜尋 (BFS) 演算法以廣度優先的方式遍歷圖，並使用佇列來記住在任何迭代中遇到死衚衕時，下一個要開始搜尋的頂點。

如上例所示，BFS 演算法首先從 A 到 B 到 E 到 F，然後到 C 和 G，最後到 D。它採用以下規則。

• 規則 1 - 訪問相鄰的未訪問頂點。將其標記為已訪問。顯示它。將其插入佇列。

• 規則 2 - 如果未找到相鄰頂點，則從佇列中刪除第一個頂點。

• 規則 3 - 重複規則 1 和規則 2，直到佇列為空。

步驟	遍歷	描述
1		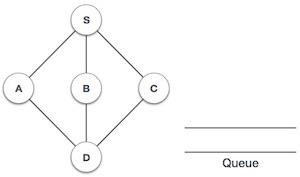初始化佇列。
2		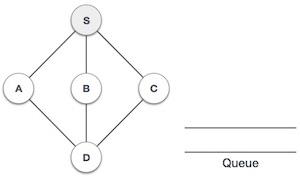我們從訪問S（起始節點）開始，並將其標記為已訪問。
3		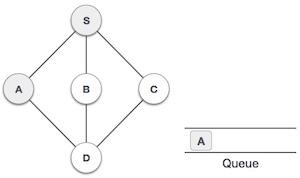然後我們從S看到一個未訪問的相鄰節點。在本例中，我們有三個節點，但按字母順序我們選擇A，將其標記為已訪問並將其入隊。
4		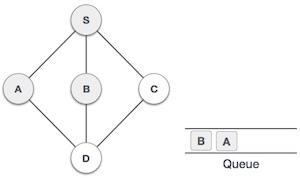接下來，S的未訪問相鄰節點是B。我們將其標記為已訪問並將其入隊。
5		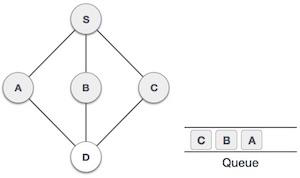接下來，S的未訪問相鄰節點是C。我們將其標記為已訪問並將其入隊。
6		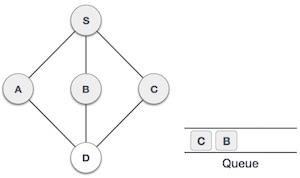現在，S沒有未訪問的相鄰節點了。因此，我們出隊並找到A。
7		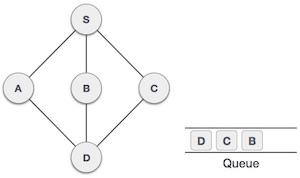從A我們有D作為未訪問的相鄰節點。我們將其標記為已訪問並將其入隊。

在這個階段，我們沒有未標記（未訪問）的節點了。但根據演算法，我們繼續出隊以獲取所有未訪問的節點。當佇列清空時，程式結束。