資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究N元樹的同構
同構定義為兩棵樹具有相同的或映象結構。在映象結構的情況下，左節點資料將始終與右節點匹配。例如，我們將取最接近映象的數字，看看它的反轉是什麼，這就是同構的真正概念。
在本文中，我們將檢查兩棵不同的二叉樹是否同構。
讓我們來看一個N元樹同構的例子：
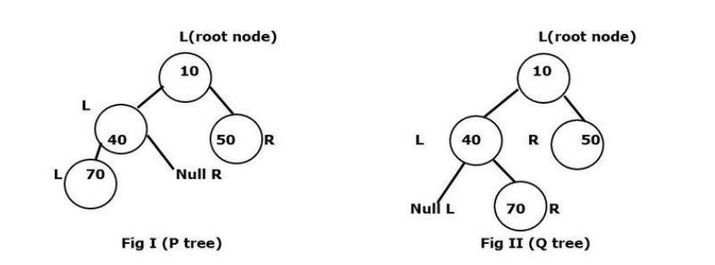
請注意，L 代表左節點，而 R 代表右節點
P 和 Q 樹在最左邊的第二個分割槽的映象結構
這兩個圖顯示了它們如何透過給出四個匹配條件（P 和 Q 的根節點）而彼此同構，例如：
左左節點可以匹配。
右右節點可以匹配。
左右節點可以匹配。
右左節點可以匹配。
語法
程式中使用的以下語法：
struct name_of_structure{
data_type var_name;
// data member or field of the structure.
}
引數
struct - 此關鍵字用於表示結構資料型別。
name_of_structure - 我們為結構提供任何名稱。
結構是在一個地方收集各種相關變數。
演算法
我們將從名為'iostream'的標頭檔案開始程式。
我們正在建立一個名為'tree_node'的結構，其整數型別為'd'，並初始化指標變數'l'和'r'分別代表左子節點和右子節點資料。
現在我們建立另一個結構，其中包含一個名為'create_node()'的函式，該函式接受一個名為'data'的引數來處理根節點的值。此外，我們使用給定的資料建立'tree_node'指標來將左子節點和右子節點指標初始化為null，並返回根節點。使用此函式，我們將插入左子節點和右子節點。
我們正在建立一個布林型別函式'check_isomorphism_tree'，以兩個tree_node指標p和q作為輸入引數並返回布林值。在其中，我們建立兩次“if 語句”來檢查p中的資料是否等於q。
檢查 p 和 q 是否都為 null，如果是，則返回 true，因為樹是同構的。
檢查 p 或 q 是否為 null，如果是，則返回 false，因為樹不是同構的。
在'check_isomorphism_tree'函式中，我們使用邏輯運算子“&&”和“||”遞迴地檢查節點'p'和'q'的左子節點和右子節點的所有可能組合。
我們從主函式開始，建立兩個樹節點'p'和'q'來提供資訊。
在主函式中，我們使用 if 語句呼叫'check_isomorphism_tree'函式，並將給定的引數 p 和 q 傳遞給它，以驗證這些整數值是否同構。如果它是同構的，則列印語句為“給定的節點資訊將構成同構樹”，否則反之。
示例
在這個程式中，我們將檢查兩棵二叉樹是否同構。
#include<iostream>
using namespace std;
struct tree_node{
int d;
tree_node*l; // l = left
tree_node*r; // r = right
};
struct tree_node* create_node(int data){
struct tree_node*root= new tree_node;
root->d= data;
root->l= NULL;
root->r= NULL;
return root;
}
bool check_isomorphism_tree(tree_node*p, tree_node*q) {
// p and q both are different tree
if(p==NULL and q==NULL){
return true;
}
if(p==NULL or q==NULL){
return false;
}
// return all the possible condition
return (p->d==q->d && ((check_isomorphism_tree(p->l,q->r)&& check_isomorphism_tree(p->r,q->l))||(check_isomorphism_tree(p->l,q->l)&& check_isomorphism_tree(p->r,q->r))));
}
int main(){
// Tree of root p
struct tree_node *p = create_node(10);
p->l = create_node(5);
p->r = create_node(4);
p->l->l = create_node(11);
p->r->r = create_node(12);
p->l->r = create_node(51);
p->r->l = create_node(6);
p->l->r->l = create_node(7); // left->right->left
p->l->l->l = create_node(9); // left->left->left
// Tree of root q
struct tree_node *q = create_node(10);
q->l = create_node(5);
q->r = create_node(4);
q->l->l = create_node(11);
q->r->r = create_node(12);
q->l->r = create_node(51);
q->r->l = create_node(6);
q->l->r->l = create_node(7);
q->l->l->l = create_node(9);
if(check_isomorphism_tree(p,q)){
cout<<"This given information of node will make isomorphism tree"<<endl;
} else {
cout<<" This given information of node will not make isomorphism tree "<<endl;
}
return 0;
}
輸出
This given information of node will make isomorphism tree
結論
在這個程式中，我們理解了 N 元樹同構的概念。我們看到了結構如何幫助表示樹節點，以及左左節點、右左節點、左右左節點等的使用如何幫助構建樹，以及以下操作如何滿足樹的同構性。
379 次瀏覽
