同構

一個圖可以以不同的形式存在，具有相同數量的頂點、邊，以及相同的邊連通性。這樣的圖稱為同構圖。請注意，在本章中，我們主要為了引用和識別圖而對圖進行標記。

同構圖

如果兩個圖 G₁ 和 G₂ 滿足以下條件，則稱它們是同構的：

• 它們的組成部分（頂點和邊）數量相同。
• 它們的邊連通性保持不變。

注意 - 簡而言之，在兩個同構圖中，一個是另一個的修改版本。無標記圖也可以被認為是同構圖。

There exists a function 'f' from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 = G2.

注意

如果 G₁ = G₂，則：

• |V(G₁)| = |V(G₂)|

• |E(G₁)| = |E(G₂)|

• G₁ 和 G₂ 的度數序列相同。

• 如果頂點 {V₁, V₂, .. V_k} 在 G₁ 中形成長度為 K 的迴圈，則頂點 {f(V₁), f(V₂),… f(V_k)} 應該在 G₂ 中形成長度為 K 的迴圈。

以上所有條件對於圖 G₁ 和 G₂ 成為同構都是必要的，但不足以證明這兩個圖是同構的。

• (G₁ = G₂) 當且僅當 (G₁− = G₂−)，其中 G₁ 和 G₂ 是簡單圖。

• (G₁ = G₂) 如果 G₁ 和 G₂ 的鄰接矩陣相同。

• (G₁ = G₂) 當且僅當 G₁ 和 G₂ 的對應子圖（透過刪除 G₁ 中的一些頂點及其在圖 G₂ 中的映像獲得）是同構的。

示例

以下哪些圖是同構的？

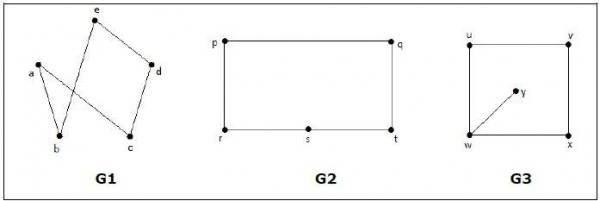
在圖 G₃ 中，頂點“w”的度數僅為 3，而其他所有圖頂點的度數均為 2。因此，G₃ 與 G₁ 或 G₂ 不同構。

取 G₁ 和 G₂ 的補圖，得到：

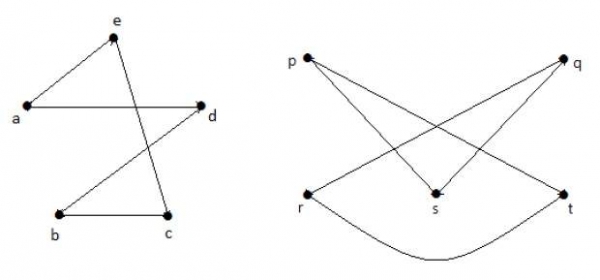
這裡，(G₁− = G₂−)，因此 (G₁ = G₂)。

Mahesh Parahar

更新於: 2019年8月23日

696 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習