截距

---

介紹

• 座標圖也稱為座標網格或平面。

• 在座標網格中，兩條垂直線稱為軸。

• 水平軸稱為x軸，垂直軸稱為y軸。

• 在網格中，點分佈在數軸上，即x軸和y軸上。

• 接觸點以有序對的形式寫出。透過讀取座標平面的經緯度，可以找到網格上點的座標。

• x軸上的點稱為x座標，y軸上的點稱為y座標。

截距

• 截距基本上是圖中交點的座標。

• 如果一條直線在一點與x軸相交，則該點稱為x截距；y截距是直線與y軸相交的點。

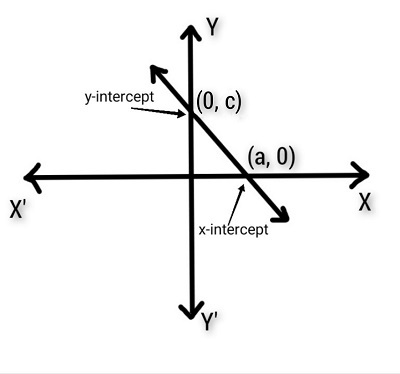
直線在座標軸上的截距

當一條直線在B點與x軸相交，在C點與y軸相交時，OB和OC分別稱為該直線在x軸和y軸上的截距。

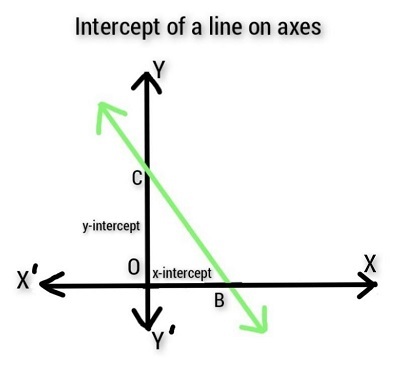
直線在圓錐曲線上的截距

一條直線在固定點與一條垂直線相交，圍繞該點旋轉形成一個稱為雙圓錐的曲面。當雙圓錐與平面相交時，會形成二維曲線。這些曲線稱為圓錐曲線。

平面與雙圓錐相交形成四種圓錐曲線。

當直線與圓錐曲線相交時，就會有解。截距將表示為有序對。

在圖中，如果一條直線與圓錐曲線不相交，則無解。這意味著在平面上找不到截距。

例如：

一條直線Ax + By = C與雙曲線 (x-h)²/a² - (y-k)²/b² = 1 相交

則直線將在點P(x₁,y₁)和Q(x₂,y₂)與雙曲線相交，其中P和Q稱為交點。

直線方程：斜率-截距式

當一條直線與座標軸相交時，它在座標圖中與一個或兩個點相交。

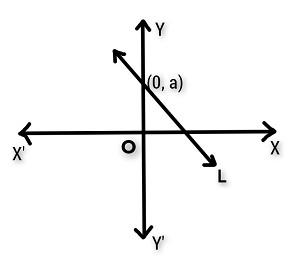
在上圖中，給定直線的y截距是距離a。

從圖的原點到直線與y軸交點的單位距離是a。

點斜式直線方程為 y - y₁ = m(x - x₁)

斜率為m且經過點(0, a)的直線方程為：

y - a = m(x - 0 其中 (0,a) 為 (x₁,y₁))

y = mx + a

因此，y = mx + a是直線的斜率-截距式方程。

直線方程：截距式

當一條直線與座標軸相交時，它在座標圖的x軸和y軸上分別與一個點相交。

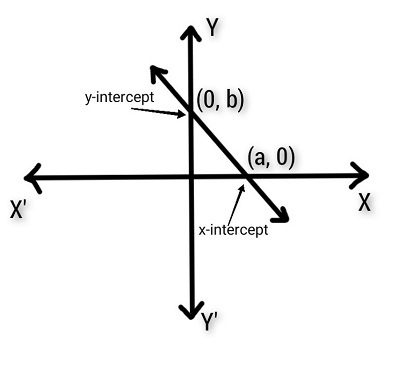
在上圖中，直線與兩點 (a,0) 和 (0,b) 相交。

兩點式直線方程為 (y - y₁) = (y₂ - y₁)/(x₂ - x₁)(x - x₁)

因此，與兩點 (a,0) (x₁,y₁) 和 (0,b) = (x₂,y₂) 相交的直線方程為：

(y - 0) = (b - 0)/(0 - a)(x - a)

-ay = bx - ab

=> bx + ay = ab .........(1)

將(1)式兩邊除以ab，得到：

bx/ab + ay/ab = ab/ab

透過約去公因式，我們得到截距式直線方程：

x/a + y/b = 1

例題

1. 從下圖中，找出直線的截距。

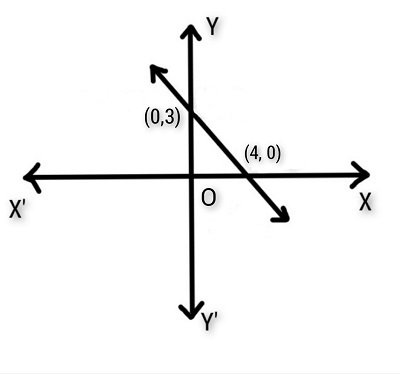
解：

直線與x軸相交於 (4,0)，與y軸相交於 (0,3)。

因此，直線在座標軸上的截距為 (4,0) 和 (0,3)。

2. 在給定的直線 7x + 9y = 14 中，求x截距和y截距。

解：

直線方程為 7x + 9y = 14

要找到該直線的x截距，令 y = 0

7x + 9(0) = 14

=> 7x = 14

x = 2

要找到該直線的y截距，令 x = 0

7(0) + 9y = 14

=> 9y = 14

y = 14/9

因此，x截距 = 2，y截距 = 14/9

如果經過 (1,2) 的直線的斜率為 -5/7

3. 求直線方程

解：

直線的斜率-截距式方程為 y = mx + a

將 m = -5/7 代入 y = mx + a，得到

2 = -5/7(1) + a

14 = -5 + a

=> a = 19

因此，直線方程為 7y = -5x + 19

4.如果直線方程為 6x + 3y = 12。將直線方程表示為截距式，並求x截距和y截距。

解：

直線方程為 6x + 3y = 12.......(1)

將(1)式兩邊除以12，得到：

6x/12 + 3y/12 = 12/12

x/2 + y/4 = 1 是直線的截距式方程

因此，x截距 = 2，y截距 = 4

結論

• 在座標圖中，水平軸稱為x軸，垂直軸稱為y軸。

• 當一條直線在一點與x軸相交時，該點稱為x截距；y截距是直線與y軸相交的點。

• x軸上的點稱為x座標，y軸上的點稱為y座標。

• 直線方程為 x/a + y/b = 1，其中a和b分別是直線的x截距和y截距。

• 直線的斜率-截距式方程為 y = mx + a

常見問題

1. 誰引入了座標系？

• 座標系，也稱為笛卡爾平面，是以法國數學家勒內·笛卡爾的名字命名的。

• 他是第一個在座標平面上引入幾何問題求解方法的人。

• 他被稱為解析幾何之父。

2. 誰發明了圓錐曲線？

希臘數學家梅內克穆斯介紹了圓錐曲線的概念。

3. 圓的一般方程是什麼？它是如何從雙圓錐形成的？

圓的一般方程為 (x - h)² + (y - k)² = a²

其中a是半徑，(h, k)是圓心。

• 圓錐曲線的底部曲面是一個圓。

• 當平面與雙圓錐水平相交時，會形成一個圓。

• 當平面垂直於軸時，橢圓會變成圓。

4. 什麼是退化圓錐曲線？

如果平面與雙圓錐的頂點相交，則形成的圖形稱為退化圓錐曲線。

5. 給出解析幾何的一些實際應用。

• 為了確保飛行安全，解析幾何用於更新航班的位置。

• 它用於收集衛星位置資訊。

• 地球的經緯度可以用座標系來描述。

• 可以用解析幾何來預測風暴未來的路徑。

• 地圖上城市和州的位置是藉助解析幾何來定位的。