資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究如何在 Python 中實現梯度下降以找到區域性最小值？
梯度下降是機器學習中一種重要的最佳化方法，用於最小化模型的損失函式。通俗地說，它涉及到反覆改變模型的引數，直到找到一組理想的值，從而使損失函式最小化。該方法透過沿著損失函式負梯度的方向（更具體地說，是沿著最陡下降路徑）進行小步調整來工作。學習率是一個超引數，它控制著演算法在速度和準確性之間的權衡，影響著步長的大小。許多機器學習方法，包括線性迴歸、邏輯迴歸和神經網路等，都使用了梯度下降。它的主要應用是在模型訓練中，目標是最小化目標變數的預測值與實際值之間的差異。在這篇文章中，我們將探討如何在 Python 中實現梯度下降以找到區域性最小值。
現在是時候在 Python 中實現梯度下降了。以下是關於我們如何實現它的基本說明：
首先，我們匯入必要的庫。
定義函式及其導數。
接下來，我們將應用梯度下降函式。
應用函式後，我們將設定引數以找到區域性最小值，
最後，我們將繪製輸出的圖形。
在 Python 中實現梯度下降
匯入庫
import numpy as np import matplotlib.pyplot as plt
然後我們定義函式 f(x) 及其導數 f'(x) -
def f(x): return x**2 - 4*x + 6 def df(x): return 2*x - 4
F(x) 是需要減小的函式，df 是它的導數 (x)。梯度下降方法利用導數來指導自身向最小值方向前進，因為它揭示了函式沿途的斜率。
然後定義梯度下降函式。
def gradient_descent(initial_x, learning_rate, num_iterations):
x = initial_x
x_history = [x]
for i in range(num_iterations):
gradient = df(x)
x = x - learning_rate * gradient
x_history.append(x)
return x, x_history
梯度下降函式接收 x 的初始值、學習率和所需的迭代次數作為輸入。它將 x 初始化為其初始值並建立一個空列表來儲存每次迭代後的 x 值。然後，該函式對給定的迭代次數執行梯度下降，根據公式 x = x - 學習率 * 梯度在每次迭代中更新 x。該函式返回每次迭代的 x 值列表以及 x 的最終值。
現在可以使用梯度下降函式來找到 f(x) 的區域性最小值 -
示例
initial_x = 0
learning_rate = 0.1
num_iterations = 50
x, x_history = gradient_descent(initial_x, learning_rate, num_iterations)
print("Local minimum: {:.2f}".format(x))
輸出
Local minimum: 2.00
在這個例子中，x 最初設定為 0，學習率為 0.1，並執行 50 次迭代。最後，我們列印 x 的值，它應該接近 x=2 處的區域性最小值。
繪製函式 f(x) 和每次迭代的 x 值的圖形，我們可以觀察到梯度下降過程。
示例
# Create a range of x values to plot
x_vals = np.linspace(-1, 5, 100)
# Plot the function f(x)
plt.plot(x_vals, f(x_vals))
# Plot the values of x at each iteration
plt.plot(x_history, f(np.array(x_history)), 'rx')
# Label the axes and add a title
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent')
# Show the plot
plt.show()
輸出
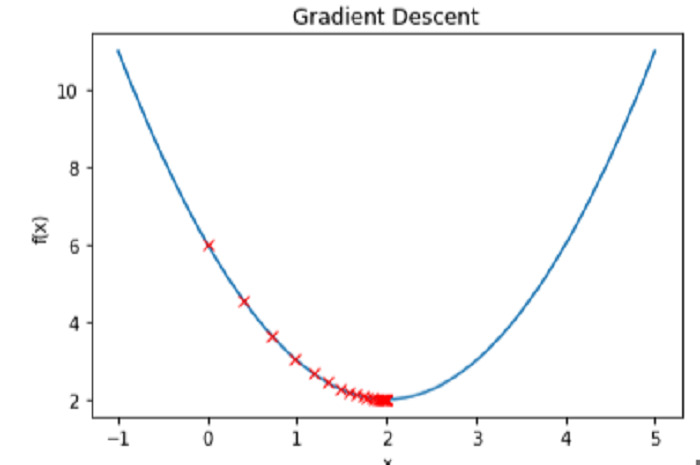
結論
總之，Python 使用稱為梯度下降的有效最佳化過程來找到函式的區域性最小值。梯度下降透過在每一步計算函式的導數，反覆更新輸入值，使其沿著最陡下降的方向移動，直到達到最小值。在 Python 中實現梯度下降包括指定要最佳化的函式及其導數、初始化輸入值以及確定演算法的學習率和迭代次數。最佳化完成後，可以透過跟蹤演算法到最小值的步驟並可視化它如何到達最小值來評估該方法。由於 Python 可以處理大型資料集和複雜的函式，因此梯度下降可以成為機器學習和最佳化應用中的有用技術。
3K+ 瀏覽量
