資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究如何計算不同型別電容器的電容？
電容 - 定義
電容器儲存電荷的能力稱為其電容。換句話說，電容也可以定義為材料的一種特性，由於它阻礙了施加在其上的電壓的任何變化。
電容：公式
實驗發現，儲存在電容器中的電荷Q與其兩端的電壓成正比，即
$$Q\propto\:V$$
$$Q=CV$$
其中，C為常數，稱為電容器的電容。
$$\Rightarrow\:C=\frac{Q}{V}$$
因此，電容器的電容(C)也可以定義為任一極板上的電荷與其兩端電壓之比。
電容單位
我們已經看到，
$$C=\frac{Q}{V}=\frac{庫侖}{伏特}=法拉$$
電容的SI單位是庫侖/伏特，也稱為法拉，用F表示。
等效電容
情況1 - 當電容器串聯連線時
參考電路圖，我們可以寫出：
$$V=V_{1}+V_{2}+V_{3}=(\frac{Q}{C_{1}}+\frac{Q}{C_{2}}+\frac{Q}{C_{3}})=Q(\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}})$$
$$\Rightarrow\:\frac{V}{Q}=(\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}})$$
$$\Rightarrow\frac{1}{C_{r}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}$$
根據此公式，可以確定串聯連線電容器的總等效電容。
情況2 - 當電容器並聯連線時
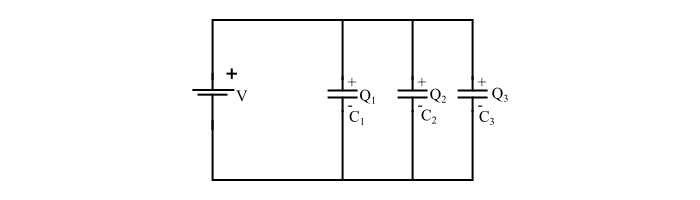
參考電路圖，可以寫出：
$$Q=Q_{1}+Q_{2}+Q_{3}=C_{1}V+C_{2}V+C_{3}V=V(C_{1}+C_{2}+C_{3})$$
$$\Rightarrow\:\frac{Q}{V}=(C_{1}+C_{2}+C_{3})$$
$$\Rightarrow\:C_{r}=C_{1}+C_{2}+C_{3}$$
以上公式給出了並聯連線電容器的總電容。
平行板電容器的電容
情況1 - 具有均勻介質
考慮一個平行板電容器，它由兩個面積為A的極板組成。兩極板之間的距離為d。兩極板之間存在空氣作為介質。
因此，平行板電容器的電容為：
與每個極板的表面積(A)成正比。
與極板之間的距離(d)成反比。
因此，
$$電容，C\propto\:\frac{A}{d}$$
$$\Rightarrow\:C=\varepsilon_{0}\frac{A}{d}$$
其中，ε0為比例常數，稱為真空或空氣的絕對介電常數，其值為8.854 × 10−12 F/m 。
如果在電容器的極板之間放置均勻的介質材料，則電容器的電容變為：
$$C=\varepsilon_{0}\varepsilon_{r}\frac{A}{d}$$
其中，εr 為介質材料的相對介電常數。
情況2 - 具有複合介質
假設電容器極板之間的空間被三種厚度分別為d1、d2和d3，相對介電常數分別為εr1、εr2和εr3的介質材料佔據。則各個部分的電容為：
$$C_{1}=\varepsilon_{0}\varepsilon_{r1}\frac{A}{d_{1}}\:;\:C_{2}=\varepsilon_{0}\varepsilon_{r2}\frac{A}{d_{2}}\:and\:C_{3}=\varepsilon_{0}\varepsilon_{r3}\frac{A}{d_{3}}$$
從圖中可以看出，這三個電容看起來像是串聯連線的，所以
$$\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}=\frac{1}{(\varepsilon_{0}\varepsilon_{r1}\frac{A}{d_{1}})}+\frac{1}{(\varepsilon_{0}\varepsilon_{r2}\frac{A}{d_{2}})}+\frac{1}{(\varepsilon_{0}\varepsilon_{r3}\frac{A}{d_{3}})}$$
$$\Rightarrow\frac{1}{C}=\frac{d_{1}}{\varepsilon_{0}\varepsilon_{r1}A}+\frac{d_{2}}{\varepsilon_{0}\varepsilon_{r2}A}+\frac{d_{3}}{\varepsilon_{0}\varepsilon_{r3}A}=\frac{1}{\varepsilon_{0}A}(\frac{d_{1}}{\varepsilon_{r1}}+\frac{d_{2}}{\varepsilon_{r2}}+\frac{d_{3}}{\varepsilon_{r3}})$$
$$C=\frac{\varepsilon_{0}A}{(\frac{d_{1}}{\varepsilon_{r1}}+\frac{d_{2}}{\varepsilon_{r2}}+\frac{d_{3}}{\varepsilon_{r3}})}$$
$$一般情況下，C=\frac{\varepsilon_{0}A}{\sum(\frac{d}{\varepsilon_{r}})}$$
多層電容器的電容
為了獲得更大的電容值，採用了多層結構。在這種結構中，電容器由交替的金屬板和薄介質片構成。奇數號極板連線在一起形成一個端子A，偶數號極板連線在一起形成第二個端子B。
參考多層（在本例中為7層）電容器的示意圖，它相當於6個並聯的電容器。因此，總電容將是單個電容器電容的6倍。如果有n個極板，那麼(n – 1)個電容器將並聯連線。因此，
$$n-層電容器的電容=(n-1)\frac{\varepsilon_{0}\varepsilon_{r}A}{d}$$
其中，
A為每個極板的面積，
d為任意兩個相鄰極板之間的距離。
圓柱形電容器的電容
圓柱形電容器（例如電纜）由兩個同軸圓柱體組成，由介質隔開。
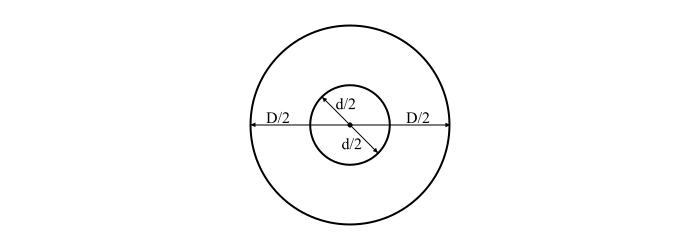
參考示意圖，圓柱形電容器的單位長度電容由下式給出：
$$C=\frac{2\pi\:\varepsilon_{0}\varepsilon_{r}}{log_{e}(\frac{D}{d})}\:F/m$$
如果電纜（圓柱形電容器）的長度為l米，則電纜的電容為
$$C=\frac{2\pi\:\varepsilon_{0}\varepsilon_{r}l}{log_{e}(\frac{D}{d})}\:法拉$$
710 次瀏覽
