使用與非門的半加器

---

在數位電子技術中，有不同型別的邏輯電路用於執行不同型別的算術運算。其中之一是加法器。**加法器**(或**二進位制加法器**)是一種組合邏輯電路，它執行兩個或多個二進位制數的加法並給出輸出和。存在兩種型別的加法器，即**半加器**和**全加器**。

由於加法器是邏輯電路，因此它們使用不同型別的數字邏輯閘來實現，例如或門、與門、非門、與非門等。在本文中，我們將討論**使用與非門實現的半加器**。但在討論之前，讓我們先了解一下半加器的基礎知識。

什麼是半加器？

一種組合邏輯電路，設計用於新增兩個二進位制數字，稱為**半加器**。半加器提供輸出以及進位值（如果有）。半加器電路透過連線一個異或門和一個與門來設計。它有兩個輸入端和兩個輸出端，分別用於求和和進位。半加器的框圖和電路圖如圖 1 所示。

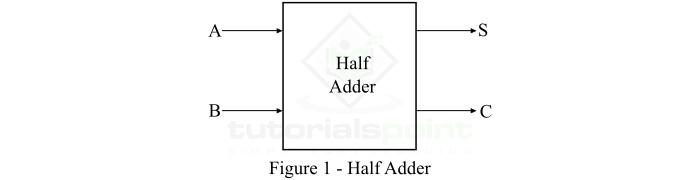
在半加器的框圖中，A 和 B 是輸入變數，S 是輸出和位，C 是輸出進位位。

半加器的真值表

以下是半加器的真值表：

輸入		輸出
A	B	S（和）	C（進位）
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

從半加器的真值表中，我們可以找到和 (S) 位和進位 (C) 位的輸出方程。這些輸出方程如下：

半加器的和 (S) 為：

$$\mathrm{Sum,\, S=AB'+A'B }$$

半加器的進位 (C) 為：

$$\mathrm{Carry,\, C=A\cdot B }$$

使用與非門的半加器

我們可以使用與非門實現半加器電路。與非門基本上是一個通用門，即它可以用於設計任何數位電路。使用與非門的半加器的實現如圖 2 所示。

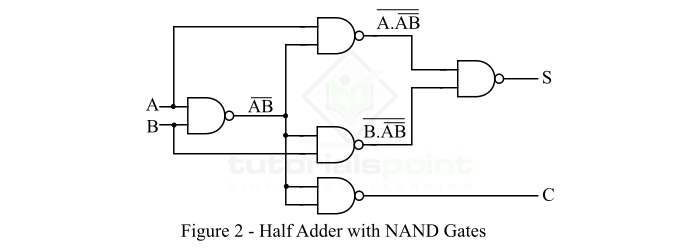
從使用與非門的半加器電路可以看出，設計半加器電路至少需要 5 個與非門。

在這裡，我們可以看到第一個與非門接收輸入位 A 和 B。第一個與非門的輸出再次作為輸入提供給 3 個與非門以及原始輸入。三個與非門中的兩個產生輸出，這些輸出再次作為輸入提供給連線在電路末端的與非門。電路末端的這個與非門給出和位 (S)。在第二階段的三個與非門中，第三個與非門生成進位位 (C)。

藉助以下方程，可以更清楚地理解使用與非門的半加器電路的操作：

$$\mathrm{Sum,\, S=((A \cdot (AB)')' \cdot (B \cdot (AB)')')'}$$

$$\mathrm{\Rightarrow Sum,\, S=((A \cdot (AB)')')' + ((B \cdot (AB)')')'}$$

$$\mathrm{\Rightarrow Sum,\, S=A \cdot (AB)' + B \cdot (AB)'}$$

$$\mathrm{\Rightarrow Sum,\, S=A \cdot (A'+B') + B \cdot (A'+B')}$$

$$\mathrm{\Rightarrow Sum,\, S=AA'+AB'+A'B+BB'}$$

$$\mathrm{\therefore Sum,\, S=AB'+A'B=A\oplus B}$$

類似地，進位位 (C) 由下式給出：

$$\mathrm{Carry,\, C=((AB)')'=AB}$$

因此，透過這種方式，我們也可以在與非邏輯中實現半加器。