圖論基礎

圖是由點和連線這些點的線組成的圖表。它至少有一條線連線一組兩個頂點，且沒有頂點連線自身。圖論中的圖的概念建立在一些基本術語之上，例如點、線、頂點、邊、頂點的度數、圖的屬性等。在本章中，我們將涵蓋圖論的這些基礎知識。

點

點是一維、二維或三維空間中的特定位置。為了更好地理解，可以用字母表示一個點。它可以用一個點表示。

示例

這裡，這個點名為“a”。

線

線是連線兩點的連線。它可以用實線表示。

示例

這裡，“a”和“b”是點。這兩個點之間的連線稱為線。

頂點

頂點是多條線相交的點。它也稱為節點。與點類似，頂點也用字母表示。

示例

這裡，頂點用字母“a”命名。

邊

邊是連線兩個頂點的線的數學術語。從單個頂點可以形成許多邊。沒有頂點，就不能形成邊。邊必須有一個起始頂點和一個結束頂點。

示例

這裡，“a”和“b”是兩個頂點，它們之間的連線稱為邊。

圖

圖“G”定義為G = (V, E)，其中V是圖中所有頂點的集合，E是圖中所有邊的集合。

示例1

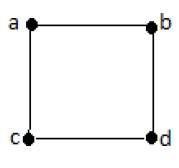
在上例中，ab、ac、cd和bd是圖的邊。類似地，a、b、c和d是圖的頂點。

示例2

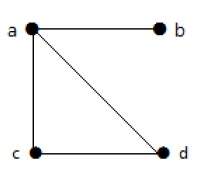
在這個圖中，有四個頂點a、b、c和d，以及四條邊ab、ac、ad和cd。

環

在圖中，如果從頂點到自身畫一條邊，則稱為環。

示例1

在上圖中，V是一個頂點，它有一條形成環的邊(V, V)。

示例2

在這個圖中，在頂點a和頂點b處形成了兩個環。

Mahesh Parahar

更新於：2019年8月23日

491 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習