資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究Go 語言二叉樹層序遍歷程式
在程式設計中，有多種資料結構用於儲存資料。資料結構主要分為線性結構和非線性結構兩種。陣列、棧、佇列和連結串列是線性資料結構。二叉樹、Trie 樹等是非線性資料結構。本文將探討非線性資料結構之一——二叉樹的層序遍歷。
層序遍歷
在二叉樹的層序遍歷中，我們從根節點開始，然後遍歷子節點，再依次遍歷子節點的子節點。以此類推，直到遍歷到最後一層，完成層序遍歷。為了實現這一點，我們使用廣度優先搜尋演算法，其中使用佇列資料結構。
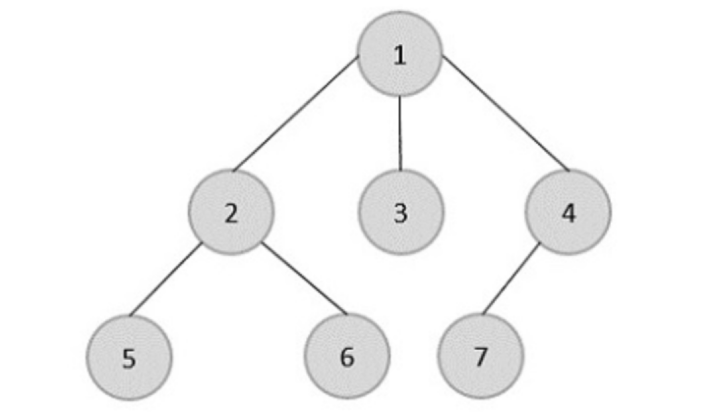
例如，在上圖所示的樹中
第 1 層：遍歷根節點 1
第 2 層：依次遍歷節點 2、節點 3 和節點 4。
第 3 層：依次遍歷節點 5、節點 6 和節點 7。
演算法
步驟 1：匯入 "fmt" - 匯入 fmt 庫
步驟 2：type TreeNode struct { Val int Left *TreeNode Right *TreeNode } - 建立一個樹節點的結構體，其中包含一個整數型別的 Val 用於儲存節點資料，以及兩個 TreeNode 型別的指標 Left 和 Right。
步驟 3：開始主函式
root : = TreeNode{0, nil, nil} - 建立一個變數 root，表示樹的根節點，型別為 TreeNode。
呼叫函式 CreateBinaryTree(&root) 建立完整的二叉樹。
levelOrder : = LevelOrderTraversal(&root) - 呼叫函式 LevelOrderTraversal 執行層序遍歷，並將根節點的引用作為引數傳遞。
列印層序遍歷函式返回的陣列。
步驟 4：層序遍歷函式。
func LevelOrderTraversal(root *TreeNode) []int {} - 宣告一個函式，TreeNode 型別的變數作為引數，返回一個整數陣列。
if root == nil { return []int{} } - 檢查根節點是否為空，如果為空則返回一個空陣列。
var q Queue - 建立一個佇列，用於實現廣度優先搜尋演算法。
var levelOrder []int - 建立一個數組，用於在層序遍歷過程中儲存節點的值。
應用廣度優先搜尋演算法，最後返回陣列。
示例
在此程式碼中，我們實現了佇列資料結構及其函式，因為目前 Go 語言中沒有預構建的佇列庫。
package main
import "fmt"
type Queue struct {
List [](*TreeNode)
}
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// function to add an element in the queue
func (q *Queue) Enqueue(element *TreeNode) {
q.List = append(q.List, element)
}
// function to delete elements in the queue
func (q *Queue) Dequeue() *TreeNode {
if q.isEmpty() {
fmt.Println("Queue is empty.")
return nil
}
element := q.List[0]
q.List = q.List[1:]
return element
}
// function checks that queue is empty or not
func (q *Queue) isEmpty() bool {
return len(q.List) == 0
}
// function to find the length of the queue
func (q *Queue) size() int {
return len(q.List)
}
// creating binary tree
func CreateBinaryTree(root *TreeNode) {
n1 := TreeNode{1, nil, nil}
n2 := TreeNode{2, nil, nil}
root.Left = &n1
root.Right = &n2
n3 := TreeNode{3, nil, nil}
n4 := TreeNode{4, nil, nil}
n1.Left = &n3
n1.Right = &n4
n5 := TreeNode{5, nil, nil}
n6 := TreeNode{6, nil, nil}
n2.Left = &n5
n2.Right = &n6
}
// level order traversal of a function with root node as argument
// and returns the right-view elements in the array
func LevelOrderTraversal(root *TreeNode) []int {
// returning empty array if the tree is empty
if root == nil {
return []int{}
}
// creating variable for queue
var q Queue
// creating array to store right side element
var levelOrder []int
// enqueue root address in the queue
q.Enqueue(root)
q.Enqueue(nil)
// breadth-first search over the tree
for q.size() > 1 {
currNode := q.Dequeue()
if currNode == nil {
q.Enqueue(nil)
levelOrder = append(levelOrder, -1)
continue
}
levelOrder = append(levelOrder, currNode.Val)
if currNode.Left != nil {
q.Enqueue(currNode.Left)
}
if currNode.Right != nil {
q.Enqueue(currNode.Right)
}
}
return levelOrder
}
func main() {
fmt.Println("Golang program to find the level order traversal of a binary tree.")
// creating root node of binary tree
root := TreeNode{0, nil, nil}
// calling CreateBinaryTree function to create a complete binary tree
CreateBinaryTree(&root)
// calling LevelOrderTraversal function
levelOrder := LevelOrderTraversal(&root)
// print elements of binary tree in level order
for i := 0; i < len(levelOrder); i++ {
if levelOrder[i] == -1 {
fmt.Println()
continue
}
fmt.Print(levelOrder[i], " ")
}
fmt.Println()
}
輸出
Golang program to find the level order traversal of a binary tree. 0 1 2 3 4 5 6
結論
透過這種方式，我們使用廣度優先搜尋演算法實現了樹的層序遍歷。樹還有其他遍歷演算法，例如中序遍歷、先序遍歷和後序遍歷。此方法的時間複雜度為 O(V + E)，其中 V 和 E 分別是圖中的頂點數和邊數。我們也可以使用深度優先搜尋演算法來查詢樹的層序遍歷。要了解更多關於 Go 語言的資訊，您可以瀏覽這些 教程。
345 次瀏覽
