
函數語言程式設計 - λ演算
λ演算是由Alonzo Church在20世紀30年代開發的一個框架,用於研究函式的計算。
函式建立 − Church引入了λx.E 表示法來表示函式,其中'x'是形式引數,'E'是函式體。這些函式可以是無名函式,並且只有一個引數。
函式應用 − Church使用E1.E2表示法來表示將函式E1應用於實際引數E2。所有函式都只有一個引數。
λ演算的語法
λ演算包括三種不同的表示式,即:
E :: = x(變數)
| E1 E2(函式應用)
| λx.E(函式建立)
其中λx.E稱為λ抽象,E稱為λ表示式。
λ演算的求值
純λ演算沒有內建函式。讓我們求值以下表達式:
(+ (* 5 6) (* 8 3))
這裡,我們不能從'+'開始,因為它只對數字進行操作。有兩個可約表示式:(* 5 6) 和 (* 8 3)。
我們可以先約簡其中一個。例如:
(+ (* 5 6) (* 8 3)) (+ 30 (* 8 3)) (+ 30 24) = 54
β-歸約規則
我們需要一個歸約規則來處理λ。
(λx . * 2 x) 4 (* 2 4) = 8
這被稱為β-歸約。
形式引數可以使用多次:
(λx . + x x) 4 (+ 4 4) = 8
當有多個項時,我們可以按如下方式處理它們:
(λx . (λx . + (− x 1)) x 3) 9
內部的x屬於內部的λ,外部的x屬於外部的λ。
(λx . + (− x 1)) 9 3 + (− 9 1) 3 + 8 3 = 11
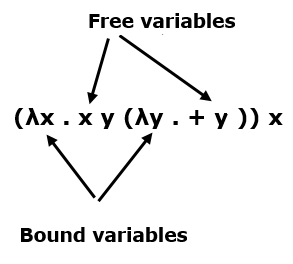
自由變數和約束變數
在一個表示式中,每個變數的出現要麼是“自由的”(對λ而言),要麼是“約束的”(對某個λ而言)。
(λx . E) y 的β-歸約將E中每個自由出現的x替換為y。例如:
α-歸約
α-歸約非常簡單,可以在不改變λ表示式的含義的情況下完成。
λx . (λx . x) (+ 1 x) ↔ α λx . (λy . y) (+ 1 x)
例如:
(λx . (λx . + (− x 1)) x 3) 9 (λx . (λy . + (− y 1)) x 3) 9 (λy . + (− y 1)) 9 3 + (− 9 1) 3 + 8 3 11
Church-Rosser定理
Church-Rosser定理陳述如下:
如果E1 ↔ E2,則存在一個E,使得E1 → E 且 E2 → E。“以任何方式歸約最終都可以產生相同的結果。”
如果E1 → E2,並且E2是正規化,則存在E1到E2的正規序歸約。“如果存在正規化,則正規序歸約將始終產生正規化。”
廣告