使用 Python 判斷是否存在長度大於 k 的路徑

假設我們有一個圖，一個源頂點和一個數字 k。k 是圖中源點到目標點之間路徑的長度，我們需要檢查是否可以找到從源點開始到任何其他頂點（作為目標點）的簡單路徑（無環）。該圖如下所示：

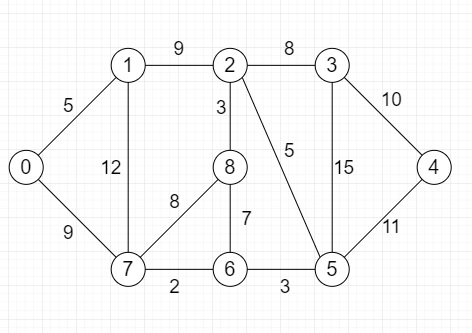
因此，如果輸入為 Source = 0，k = 64，則輸出為 True，因為存在一條從 0 到 7 到 1 到 2 到 8 到 6 到 5 到 3 到 4 的簡單路徑，這條路徑的總距離為 68，大於 64。

為了解決這個問題，我們將遵循以下步驟：

  • 使用 nodes x nodes 階的鄰接矩陣 adj 定義圖，並填充邊權重。

  • 定義一個函式 solve()。它將接收源點、k 和路徑。

  • 如果 k <= 0，則

    • 返回 True

  • i := 0

  • 當 i 不等於 adj[source] 的大小之前，執行：

    • v := adj[source, i, 0]

    • w := adj[source, i, 1]

    • i := i + 1

    • 如果 path[v] 為 True，則

      • 跳過本次迭代

    • 如果 w >= k，則

      • 返回 True

    • path[v] := True

    • 如果 solve(v, k-w, path) 為真，則

      • 返回 True

    • path[v] := False

  • 返回 False

  • 在主方法中，執行以下操作：

  • path := 一個大小與 nodes 相同的列表，然後填充假值

  • path[source] := 1

  • 返回 solve(source, k, path)

示例

讓我們來看一下以下實現，以便更好地理解：

線上演示

class Graph:
   def __init__(self, nodes):
      self.nodes = nodes
      self.adj = [[] for i in range(nodes)]
   def insert_edge(self,u, v, w):
      self.adj[u].append([v, w])
      self.adj[v].append([u, w])
   def solve(self,source, k, path):
      if (k <= 0):
         return True
      i = 0
      while i != len(self.adj[source]):
         v = self.adj[source][i][0]
         w = self.adj[source][i][1]
         i += 1
         if (path[v] == True):
            continue
         if (w >= k):
            return True
         path[v] = True
         if (self.solve(v, k-w, path)):
            return True
         path[v] = False
      return False
   def is_there_any_path(self,source, k):
      path = [False]*self.nodes
      path[source] = 1
      return self.solve(source, k, path)

nodes = 9
g = Graph(nodes)
g.insert_edge(0, 1, 5)
g.insert_edge(0, 7, 9)
g.insert_edge(1, 2, 9)
g.insert_edge(1, 7, 12)
g.insert_edge(2, 3, 8)
g.insert_edge(2, 8, 3)
g.insert_edge(2, 5, 5)
g.insert_edge(3, 4, 10)
g.insert_edge(3, 5, 15)
g.insert_edge(4, 5, 11)
g.insert_edge(5, 6, 3)
g.insert_edge(6, 7, 2)
g.insert_edge(6, 8, 7)
g.insert_edge(7, 8, 8)
source = 0
k = 64
print(g.is_there_any_path(source, k))

輸入

nodes = 9
g = Graph(nodes)
g.insert_edge(0, 1, 5)
g.insert_edge(0, 7, 9)
g.insert_edge(1, 2, 9)
g.insert_edge(1, 7, 12)
g.insert_edge(2, 3, 8)
g.insert_edge(2, 8, 3)
g.insert_edge(2, 5, 5)
g.insert_edge(3, 4, 10)
g.insert_edge(3, 5, 15)
g.insert_edge(4, 5, 11)
g.insert_edge(5, 6, 3)
g.insert_edge(6, 7, 2)
g.insert_edge(6, 8, 7)
g.insert_edge(7, 8, 8)
source = 0
k = 64

輸出

True

更新於：2020年8月25日

151 次瀏覽

開啟您的 職業生涯

完成課程獲得認證

開始學習
廣告
© . All rights reserved.