在標記鄰居的最短路徑後查詢圖中所有剩餘的頂點

---

關於圖搜尋演算法的演算法遍歷圖以尋求廣泛的發現或目標搜尋。這些演算法在網路中切割路徑，但沒有人期望這些路徑在計算上是最優的。尋路演算法也構建在圖搜尋技術之上，因為它們探索頂點之間的路徑，從特定節點開始，並透過連線直到訪問目標。

什麼是圖？

圖是反映一組元件之間“連線”的資料結構。

這些專案稱為節點。邊是節點之間的連線。

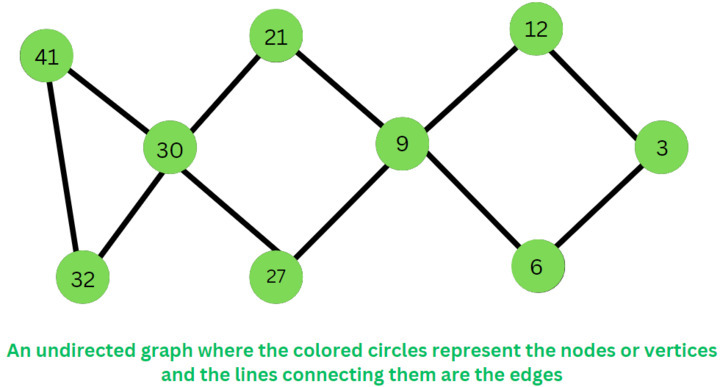
最短路徑

最短路徑演算法找到任意兩個節點或頂點之間最短的路徑或權重最小的邊。因為它即時執行，所以非常適合使用者互動和動態工作流程。

演算法型別	功能	使用示例
最短路徑變體	找到兩個頂點之間的最短路徑。	獲取跨不同點的駕車路線
"單源最短路徑"	找到根節點與所有其他節點之間的最短路徑。	最便宜的呼叫路線
"所有節點對最短路徑"	找到圖中任意兩個節點之間的最短路徑。	考慮其他路徑以避免交通擁堵。

迪傑斯特拉演算法

迪傑斯特拉演算法構建一組從源到目標距離最小的節點，以從單個源節點獲得“最短路徑樹”。

迪傑斯特拉演算法的基本原理是什麼？

迪傑斯特拉演算法的基本原理如下所示：

• 迪傑斯特拉演算法從您指定的節點（也稱為起始節點）開始，然後繼續分析圖以發現連線該頂點和圖中所有其他節點的最短路徑。

• 此技術跟蹤源節點和每個節點之間的最短距離，並在找到更短的路徑時更改值。

• 一旦找到連線源和另一個節點的最小距離，該頂點就會被標記為“已訪問”並新增到路徑中。

• 重複此過程，直到圖中的所有頂點都包含在路徑中。因此，建立了透過到每個節點的最短可行路徑將主節點連線到每個節點的路徑。

注意

圖分析在描述連結和路徑時會使用術語，例如：

• "權重" - 關係特定特徵的數值實體。

• "成本" - 在評估路徑的總權重時，我們會經常遇到它。

• "距離" 是連線屬性的常用名稱，它反映了在演算法中兩個節點之間行進的距離。

• "跳數" 指兩個頂點之間的連線數。

迪傑斯特拉演算法的主要用途

此方法在 GPS 裝置中確定當前位置和目標位置之間的最短路徑。它在行業中有多種用途，主要是在需要網路建模的領域。

如果圖的邊具有負權重，迪傑斯特拉演算法是否可以工作？

答案是否定的。

迪傑斯特拉演算法只能用於具有正權重的圖。這是因為必須新增邊的權重才能檢測最短路徑。

對於具有負權重的圖，該演算法將無法正常工作。當一個節點被標記為“已訪問”時，通向該節點的當前路徑成為最短路徑。負權重可能會改變這一點，因為總權重將在此階段之後減少。

在完成標記圖中鄰居的最短路徑以識別所有剩餘頂點後該怎麼辦？

該過程是遍歷每個頂點並用最低列號的節點標記該節點，透過權重最小的邊連線到主頂點。然後找到連線到當前節點的權重最小的邊，然後找到每個未標記的邊。

要克服此問題，請按照以下步驟操作

使用兩個迴圈 j 和 i 遍歷整個鄰接矩陣。

對於每個（行），找到鄰接矩陣中的最小結果；列號最小的節點透過權重最小的邊連線到主頂點。

使用布林陣列，為每個頂點標記此頂點。

列印布林陣列中未標記的每個頂點或節點。

此方法的實現如下

示例

#include <iostream>
#include <string>
#include <vector>
#include <limits>
 
// Stdc++11 code to implement the approach
class GFG{
   
   // Function to calculate the number of unmarked edges
   public:
   static std::vector<bool> markedNodesCounter(std::vector<std::vector<int>> &A, int V){
       
      // Initialising visited array
      std::vector<bool> marked(V);
       
      // Loop to iterate through every node
      for (int i = 0; i < V; i++){
           
         // Initialising the minimum distance and the node closest to the current node
         int minweight = std::numeric_limits<int>::max();
         int min = V + 1;
           
         // loop to find the weights from current node to every other node
         for (int j = 0; j < V; j++){
            if (i == j){
               continue;
            }
            if (A[i][j] < minweight){
               minweight = A[i][j];
               min = j;
            }
         }
         // Marking the closest node
         marked[min] = true;
      }
      // Returning the answer
      return marked;
   }
   // Driver Code
   static void main(std::vector<std::string> &args){
      int V = 3;
      std::vector<std::vector<int>> A{{0, 10, 50}, {10, 0, 30}, {50, 30, 0}};
      // Getting the result
      std::vector<bool> marked = GFG::markedNodesCounter(A, V);
      // Printing the result
      bool flag = false;
      for (int i = 0; i < V; i++){
         if (!marked[i]){
            std::cout << std::to_string(i) + " ";
            flag = true;
         }
      }
      if (!flag){
         std::cout << "-1" << std::endl;
      }else{
         std::cout << std::endl;
      }
   }
};
int main(int argc, char **argv){
   std::vector<std::string> parameter(argv + 1, argv + argc);
   GFG::main(parameter);
   return 0;
};

輸出

根據以上程式碼：

2

輔助空間為 O(V)，時間複雜度為 O(V2)，用於生成一個大小為 V 的額外陣列，並初始化兩個分別從 0 到 V 的巢狀迴圈。

哪些情況需要最短路徑？

使用最短路徑演算法，您可以根據跳數或任何其他加權連線值確定兩個節點之間的最佳路徑。它可以提供有關分離程度、兩個位置之間的最小路徑或最便宜路徑的即時響應。還可以使用此方法來調查特定節點之間的關係。

結論

尋路演算法可以幫助我們理解資料之間的關係。迪傑斯特拉演算法發現網路中兩個節點之間的最短路徑。此方法使用邊權重來檢測將主頂點連線到所有頂點的總權重最小的路徑。