迪傑斯特拉演算法計算圖中的最短路徑
定義
迪傑斯特拉演算法查詢從特定節點(稱為源節點)到連線圖中所有其他節點的最短路徑。它生成一個以源節點為根的最短路徑樹。它廣泛用於計算機網路中,目的是生成最佳路由以最大限度地降低路由成本。
迪傑斯特拉演算法
輸入 - 表示網路的圖;和一個源節點 s
輸出 - 一個最短路徑樹 spt[],以 s 作為根節點。
初始化 -
大小為 **|V|**(節點數)的距離陣列 **dist[]**,其中 **dist[s]** = **0** 且 **dist[u]** = ∞(無限),其中 u 表示圖中除 s 之外的節點。
一個數組 **Q**,包含圖中的所有節點。當演算法執行完成時,**Q** 將變為空。
一個空集 **S**,將訪問過的節點新增到其中。當演算法執行完成時,**S** 將包含圖中的所有節點。
當 **Q** 不為空時重複 -
從 **Q** 中移除具有最小 **dist[u]** 值且不在 S 中的節點 u。在第一次執行中,移除 **dist[s]**。
將 u 新增到 S,標記 u 為已訪問。
對於每個與 u 相鄰的節點 v,更新 dist[v] 為 -
如果 (**dist[u]** **+ u-v 邊權重**) **< dist[v]**,則
更新 **dist[v] = dist[u] + u-v 邊權重**
陣列 **dist[]** 包含從 s 到每個其他節點的最短路徑。
示例
可以使用示例最好地理解演算法的工作原理。考慮以下圖,其節點標記為 A 到 G,由帶權邊連線如下:
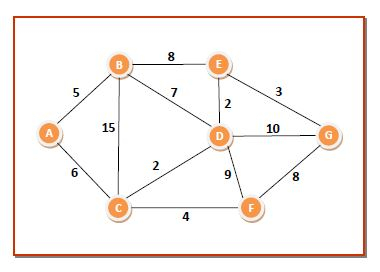
初始化如下:
dist[7]={0,∞,∞,∞,∞,∞,∞}
Q={A,B,C,D,E,F,G}
S = ∅
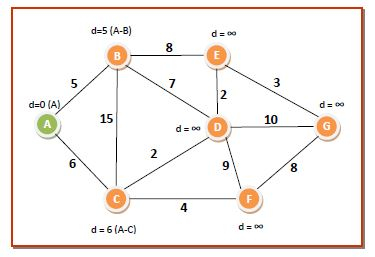
**第一輪** - 我們從 **Q** 中選擇節點 **A**,因為它具有最低的 **dist[]** 值 **0**,並將其放入 S。A 的相鄰節點是 B 和 C。我們根據演算法更新對應於 B 和 C 的 dist[] 值。因此,資料結構的值變為:
dist[7]={0,5,6,∞,∞,∞,∞}
Q={B,C,D,E,F,G}
S={A}
此輪後的距離和最短路徑如下圖所示。綠色節點表示已新增到 S 的節點:
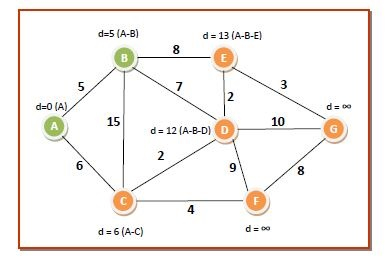
**第二輪** - 我們從 **Q** 中選擇節點 **B**,因為它具有最低的 **dist[]** 值 **5**,並將其放入 **S**。B 的相鄰節點是 **C**、**D** 和 **E**。我們根據演算法更新對應於 **C**、**D** 和 E 的 dist[] 值。因此,資料結構的值變為:
dist[7]={0,5,6,12,13,∞,∞}
Q={C,D,E,F,G}
S={A,B}
此輪後的距離和最短路徑為:
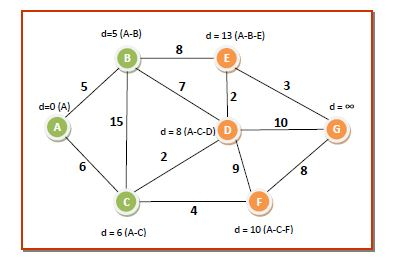
**第三輪** - 我們從 **Q** 中選擇節點 **C**,因為它具有最低的 dist[] 值 6,並將其放入 S。C 的相鄰節點是 D 和 F。我們更新對應於 D 和 F 的 dist[] 值。因此,資料結構的值變為:
dist[7]={0,5,6,8,13,10,∞}
Q={D,E,F,G}
S={A,B,C}
此輪後的距離和最短路徑為:
**第四輪** - 我們從 **Q** 中選擇節點 **D**,因為它具有最低的 **dist[]** 值 8,並將其放入 S。D 的相鄰節點是 E、F 和 G。我們更新對應於 **E**、**F** 和 **G** 的 **dist[]** 值。因此,資料結構的值變為:
dist[7]={0,5,6,8,10,10,18}
Q={E,F,G}
S={A,B,C,D}
此輪後的距離和最短路徑為:
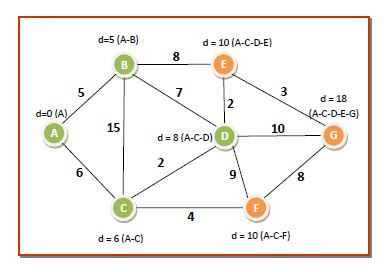
**第五輪** - 我們可以從 **Q** 中選擇節點 E 或節點 **F**,因為它們都具有最低的 **dist[]** 值 **10**。我們選擇其中一個,例如 **E**,並將其放入 **S**。**D** 的相鄰節點是 **G**。我們更新對應於 G 的 **dist[]** 值。因此,資料結構的值變為:
dist[7]={0,5,6,8,10,10,13}
Q={F,G}
S={A,B,C,D,E}
此輪後的距離和最短路徑為:
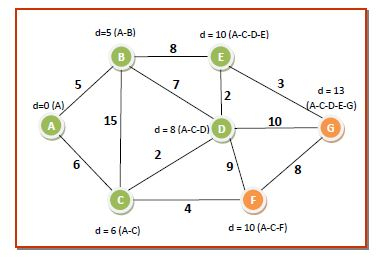
**第六輪** - 我們從 **Q** 中選擇節點 **F**,因為它具有最低的 **dist[]** 值 **10**,並將其放入 **S**。**F** 的相鄰節點是 **G**。透過 **F** 的 **dist[]** 值小於透過其他路徑的值。所以它保持不變。資料結構的值變為:
dist[7]={0,5,6,8,10,10,13}
Q={G}
S={A,B,C,D,E,F}
此輪後的距離和最短路徑為:
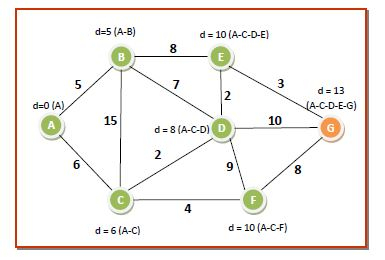
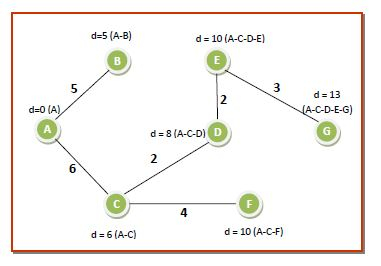
**第七輪** - **Q** 中只有一個節點。我們將其從 **Q** 中移除並放入 S。dist[] 陣列無需更改。現在,**Q** 變為空,**S** 包含所有節點,因此我們到達演算法的結尾。我們消除了不在任何路徑路徑中的所有邊或路徑。因此,從源節點 A 到所有其他節點的最短路徑樹如下:


 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP