糾錯碼中的漢明碼
當我們考慮具有相同長度的兩個碼字時,漢明碼可用於任何長度的資料單元。兩個碼字之間的漢明距離表示其特定項不同的位置數。
示例
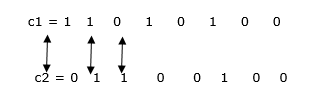
漢明距離為3。
漢明碼也稱為線性分組碼。(n, k) 漢明碼系列由 m 定義。
分組長度 n = 2m - 1。
訊息位數 k = 2m - m - 1。
奇偶校驗位數 = n - k = m。
其中 m ≥ 3
最小距離min = 3。
位元速率 = 碼效率 = $\frac{k}{n} = \frac{2^{m}-m-1}{2^{m}-1} = 1 - \frac{m}{2^{m}-1}$ 當 m >> 1 時
則位元速率 r = 1,其中 k 是訊息位,n 是每個分組傳輸的位數。
結構
奇偶校驗(冗餘)位插入到資料單元之間或資料單元的末尾。
為了評估,需要多個冗餘位來準確表示給定的資料位數 m。我們應該找到 m 和 r 之間的關係。
如果總傳輸量為 m + r,則 r 必須表示 m + r + 1 個不同的狀態。一個狀態定義為無錯誤,m + r 個狀態表示 m + r 個位置中每個位置的錯誤位置。
因此,r 位應發現 m + r + 1 個狀態,而 r 位可以表示 2r 個多個狀態。所以 2r ≥ m + r + 1。
假設 m = 7,則滿足此方程式的最小 r 值為 4。
| 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| d | D | r4 | D | D | D | D | r3 | D | r2 | r1 |
在這個 r 位放在 2n 位置上。例如,20 = 1,21 = 2,22 = 4 等位置
在漢明碼中,每個 r 位都是 VRC(垂直冗餘校驗)。
r1 位是透過使用所有二進位制表示在最右位置包含 1 的位位置計算的,即 1, 3, 5, 7, 9, 11。
r2 位是透過使用在 2, 3, 6, 7, 10, 11 位置具有 1 的所有位置計算的,依此類推。r3 位將處理 4, 5, 6 位置的位。r4 在 8, 9, 10, 11 位置進行校驗。
示例
1011
11 1001 0111 0101 0011 0001
| d | D | D | r4 | d | d | d | r3 | d | r2 | r1 |
r2 將負責它
1011 1010
11 10 0111 0110 0111 0010
| d | D | D | r6 | d | d | d | r4 | d | r2 | r1 |
等等。
計算 r 值
我們將原始字元的每個位放在 11 位單元的合適位置。我們可以計算多個位組合的偶校驗。每個合併的校驗值是相關 r 位的值。
示例
計算支援合併位 3、5、7、9、11 等的偶校驗。最後 11 位程式碼透過傳輸線路傳送。


 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP