電通量

---

簡介

卡爾·弗里德里希·高斯被廣泛認為是有史以來最偉大的數學家之一。有些人認為他是最偉大的。高斯發現了一種思考庫侖定律的方法，使我們能夠以直接的方式計算電荷分佈的電場。雖然高斯並沒有發現新的物理定律，但他對庫侖定律的重新表述同樣重要。在本教程中，我們將描述電通量、電通量的概念、電場的通量、電通量的單位和量綱公式。

為了理解高斯定律，我們必須首先掌握穿過表面的電通量的概念。這是一種計算穿過表面的總電場的方法。

什麼是電通量？

電通量以庫侖為單位測量，描述了正電荷和負電荷之間相關的力。電通量可以用從正電荷發出並終止於負電荷的通量線來表示。透過電通量來測量發射電力的表面。

電通量的概念

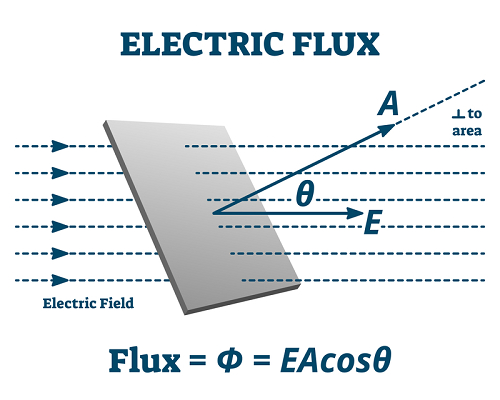
表面用於表示電通量，以及每個點的電場值。為了演示如何確定通量，讓我們從一個簡單的例子開始。一個恆定的電場（具有相同的向量值）作用在一個面積為 A 的平面上。

面積向量 *A* 表徵了該表面。這是一個大小為 A 的向量，垂直於表面。

實際上，這裡有一個小問題：就向量 A 而言，只有兩種選擇。如果選擇這個方向，無論它指向相反的方向，它都將垂直於表面且具有相同的大小。但是，在每個涉及電通量的題目中，選擇的方向都是顯而易見的。

在這個簡單的情況下，電通量 φ 由下式給出：

$$\mathrm{\phi =E.A=EAcos\theta }$$

通常，對於非平坦的表面，可能需要使用高階微積分方法來找到通量，並且電場在該表面上不會是均勻的（大小或方向）。但是，基本思想很簡單。如果我們將表面分成足夠小的部分（例如，正方形），以便對電場進行合理的表示，那麼將表面視為平坦的，並將電場視為連續的，是一個很好的近似值。假設第 i 個正方形的面積為 ΔAi，並且電場接近於 Ei。則小正方形的電通量為：

$$\mathrm{\Delta \phi_{i} =\Delta E_{i}.A_{i}}$$

為了得到整個表面的總電通量，近似等於將所有單個貢獻相加。

$$\mathrm{\Delta \phi_{i} \approx\sum_{i}^{} \Delta E_{i}.A_{i}}$$

透過增加小正方形的數量並減小它們的大小，我們可以接近電通量 φ 的真實值。在微積分中，也可以使用類似的過程計算（一個變數的）積分。在這裡，我們得到一個曲面積分，並且在表面 S 上的電通量為：

$$\mathrm{\phi =\oint E.dA}$$

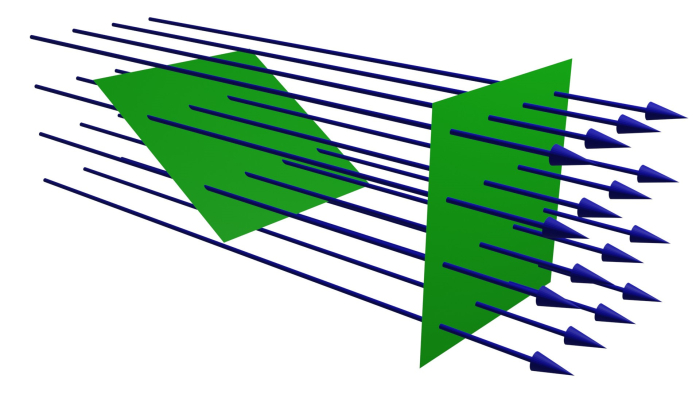
電場的通量

這是一個最簡單的例子：電場是恆定的，表面垂直於它。透過將表面積 A 乘以電場強度，計算穿過表面的電通量。

$$\mathrm{\phi = E.A}$$

在這種情況下，通量測量有多少條場線穿過表面。如果表面傾斜一定角度，預計穿過表面的線會更少。如果它平行於這些線，則沒有任何東西穿過表面。

定義為穿過其法線與場線成一定角度的表面的通量為：

$$\mathrm{\phi = EAcos\theta }$$

每個表面都有一個與其相關的法線方向。表面的面積可以被認為是一個具有法線方向的向量。通量是透過取電場和該面積向量的點積來計算的。

$$\mathrm{\phi = E.A}$$

電場具有一種稱為電通量的特性，它是穿過給定面積的力線的數量。假設電場線始於正電荷，終止於負電荷。

指向封閉表面的場線為負，而指向封閉表面外的場線為正。當封閉表面上沒有淨電荷時，場線穿過其內部，並在其他地方向外指向。當淨通量為零時，或者負通量的大小等於正通量的大小時，電通量的大小相等。

電通量的單位和量綱公式

電通量以庫侖為單位測量，描述了正電荷和負電荷之間相關的力。電通量可以用從正電荷發出並終止於負電荷的通量線來表示。透過電通量來測量發射電力的表面。

電通量的單位是 \(\mathrm{\frac{牛頓\times 米^{2}}{庫侖}}\) 或 \(\mathrm{\frac{Nm^{2}}{c}}\)，量綱是 \(\mathrm{\left [ M^{1}L^{3}T^{-3} I^{-1}\right ]}\)。

結論

電通量取決於穿過電場中給定區域的線數。假設這些線始於正電荷，終止於負電荷。正場線指向封閉表面內部，而負場線指向封閉表面外部。在本教程中，我們描述了電通量、電通量的概念、電場的通量、電通量的單位和量綱公式。

常見問題

Q1. 電通量受距離影響嗎？

A1. 通量與距離 r 無關。圍繞點電荷的封閉表面將產生相同的結果，無論其大小如何。

Q2. 波的通量是什麼意思？

A2. 它是透過垂直於波傳播方向的特定區域的能量量。它用 *S* 表示。

Q3. 能有負通量嗎？

A3. 請記住，穿過表面的電場線的數量與通量成正比。電場線將進入或離開封閉表面，因此相應的通量將為正或負。

Q4. 電通量的意義是什麼？

A4. 電通量的物理意義在處理位移電流的安培-麥克斯韋定律中得到了揭示。需要電通量來解釋電容電路中的電流連續性。

Q5. 通量受速度影響嗎？

A5. 通量等於垂直於場投影的面積和場的幅度。在這種情況下，只有當平面相對於場的方向改變其方向時，通量才會改變。因此，最終答案是，在這種情況下，通量與速度無關。