一維和二維彈性碰撞與非彈性碰撞

---

介紹

在我們的日常生活中，我們經歷了各種各樣的碰撞。例如，在板球運動中，球與球棒發生碰撞。碰撞前，球和球棒的方向彼此相對，碰撞後，球的能量、速度和方向都會發生變化。在碰撞過程中，粒子之間的相互作用時間很短，但作用力相對較大。碰撞可以是彈性的，也可以是非彈性的。

什麼是彈性碰撞？

在彈性碰撞過程中，發生碰撞的物體的動能或線性動量保持不變，或者簡單地說，動能是守恆的，這意味著沒有動能損失。粒子的碰撞是彈性的。

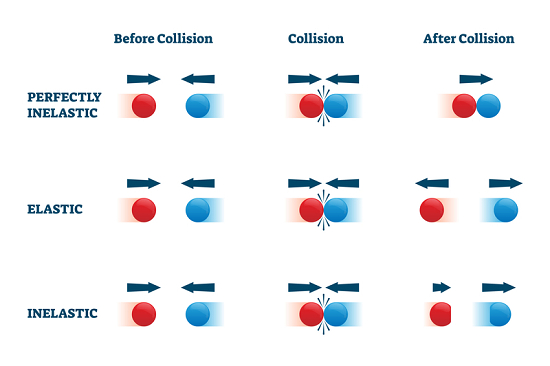
什麼是非彈性碰撞？

在非彈性碰撞過程中，系統的動能會損失，這意味著能量不守恆，粒子會粘在一起然後一起運動。動量保持守恆。初始動能總是大於最終動能。

碰撞型別

主要有兩種型別的碰撞：一種是彈性碰撞，另一種是非彈性碰撞。在第一種情況下，動能保持不變，而在第二種情況下，動能不守恆。

線性動量守恆定律

我們知道，動量被測量為物體的質量和速度的乘積。現在，根據線性動量守恆定律，如果一個物體與另一個物體發生碰撞，則碰撞前物體的總動量等於或等於碰撞後物體的總動量。

設碰撞前的初始速度為 $\mathrm{u_1}$ 和 $\mathrm{u_2}$。碰撞後的最終速度為 $\mathrm{v_{1}}$ 和 $\mathrm{v_{2}}$。質量是恆定的，因此碰撞後質量保持不變。力有大小相等、方向相反的反作用力。

$$\mathrm{F_1=-F_2}$$

$$\mathrm{m_1 a_1=-m_2 a_2}$$

$$\mathrm{m_1\frac{(v_{1}-u_{1})}{t}=-m_2\frac{(v_{2}-u_{2})}{t}}$$

時間t被消去了

$$\mathrm{m_1 v_{1}-m_1 u_1=-m_2 v_{2}+m_2 u_2}$$

$$\mathrm{m_1 v_{1}-m_1 u_1=m_2 u_{2}-m_2 v_2}$$

$$\mathrm{m_1 v_{1}+m_2 v_2=m_2 u_{2}+m_1 u_1}$$

或者 $$\mathrm{m_1 u_{1}+m_2 u_2=m_1 v_{1}+m_2 v_2}$$

因此，碰撞前的總動量等於或等於碰撞後的總動量。

一維彈性碰撞

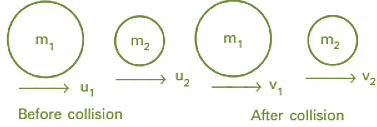
圖：1 一維彈性碰撞

假設兩個物體或物體的質量分別為 $\mathrm{m_1}$ 和 $\mathrm{m_2}$，它們以直線或勻速運動，初始速度分別為 $\mathrm{u_{1}}$ 和 $\mathrm{u_{2}}$（$\mathrm{u_{1}}$ 大於 $\mathrm{u_{2}}$），碰撞後物體的速度變為 $\mathrm{v_1}$ 和 $\mathrm{v_2}$（$\mathrm{v_2}$ 大於 $\mathrm{v_1}$）

根據動量守恆定律，

$$\mathrm{m_1 u_{1}+m_2 u_2=m_1 v_{1}+m_2 v_2}$$

$$\mathrm{m_1 u_{1}-m_1 v_1=m_2 v_{2}-m_2 u_2}$$

$$\mathrm{m_1(u_{1}-v_1)=m_2 (v_2-u_2) \:\:\: ….(1)}$$

根據能量守恆定律，動能守恆

$$\mathrm{\frac{1}{2}m_1u_1^{2}+\frac{1}{2}m_1u_2^{2}=\frac{1}{2}m_2v_1^{2}+\frac{1}{2}m_2v_2^{2}}$$

$$\mathrm{\frac{1}{2}m_1u_1^{2}-\frac{1}{2}m_1v_1^{2}=\frac{1}{2}m_2v_2^{2}-\frac{1}{2}m_2u_2^{2}}$$

$$\mathrm{\frac{1}{2}m_1(u_1^{2}-v_1^{2})=\frac{1}{2}m_2(v_2^{2}-u_2^{2})}$$

$$\mathrm{m_1(u_1^{2}-v_1^{2})=m_2(v_2^{2}-u_2^{2})\:\:\:\:….(2)}$$

將公式 (2) 除以 (1)

$$\mathrm{\frac{m_1(u_1^{2}-v_1^{2})}{m_1(u_1-v_1)}=\frac{m_2(v_2^{2}-u_2^{2})}{m_2(v_2-u_2)}}$$

$$\mathrm{\frac{(u_1 +v_1 )((u_(1 )-v_1)}{(u_(1 )-v_1)}=\frac{(v_2 -u_2 )(v_2+u_2)}{(v_2-u_2)}}$$

(因為相同的值被消去了)

$$\mathrm{(u_1+v_1)=(v_2+u_2)}$$

$$\mathrm{(u_1 -u_2)=(v_2-v_1)}$$

因此，碰撞前的相對速度 $\mathrm{(u_1-u_2)}$ 等於碰撞後的相對速度 $\mathrm{(v_2-v_1)}$。

二維彈性碰撞

根據能量守恆定律，

碰撞前的總動能(KE)總是等於或等於碰撞後的總動能(KE)。

$$\mathrm{\frac{1}{2}m_1u_1^{2}+\frac{1}{2}m_1u_2^{2}=\frac{1}{2}m_2v_1^{2}+\frac{1}{2}m_2v_2^{2}}$$

(1/2 將被消去，所以我們有)

$$\mathrm{m_1 u_1^{2}+m_1 u_2^{2}=m_2 v_1^{2}+m_2 v_2^{2}}$$

由於線性動量是恆定的，

碰撞前的匯流排性動量與碰撞後的匯流排性動量相同。對於水平分量

$$\mathrm{m_1 u_{1}+m_2 u_2=m_1 v_{1}\:cos \theta +m_2 v_2\:cos \theta}$$

對於垂直分量

$$\mathrm{0=m_1 v_{1} sin \theta +m_2 v_2 sin \theta}$$

四個未知量，即 $\mathrm{m_1,m_2,v_1,u_2,\theta}$，透過測量四個未知量中的一個，可以求解其他三個未知量的值。

一維非彈性碰撞

在非彈性碰撞中，物體粘在一起並以相同的速度沿相同的方向運動。動量守恆，但動能可能發生變化並轉變為不同型別的能量。由於物體粘在一起，動量守恆為：

$$\mathrm{m_1 u_{1}+m_2 u_2=(m_1+m_2)v}$$

這裡最終速度變為 v，我們找到 v 的值為

$$\mathrm{v=\frac{m_1 u_{1}+m_2 u_2}{(m_1+m_2)}}$$

此外，動能損失由下式給出：

$$\mathrm{KE=\frac{1}{2}m_1u_{2}-\frac{1}{2}(m_1+m_2)v_2}$$

二維非彈性碰撞

我們知道，任何粒子的系統的匯流排性動量將保持恆定，這意味著總初始動量等於總最終動量。

我們有，

$$\mathrm{m_1 u_{1}+m_2 u_2=m_1 v_{1}\:cos \theta +m_2 v_2\:cos\theta}$$

$$\mathrm{0=m_1 v_{1} sin \theta-m_2 v_2 sin\theta}$$

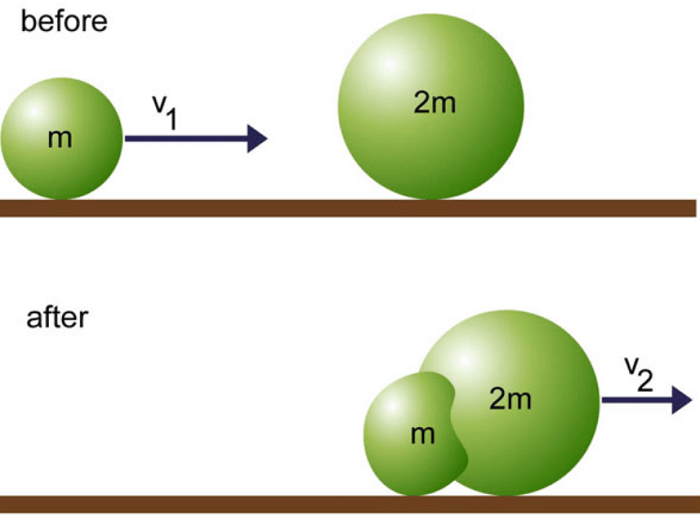
二維非彈性碰撞

由於物體粘在一起，

$$\mathrm{m_1 u_{1}cos \theta +m_2 u_2=(m_1+m_2)v\:cos \theta}$$

因此，左側的動量等於右側的線性動量，即最終動量。所以這是完全非彈性碰撞的方程。碰撞後速度變為相同。因此，最終速度表示為 v。

一維和二維碰撞的例子

一些與碰撞相關的例子是

• 當你將籃球擊打在地面上時，它會彈回你的身邊。在這種情況下，動能保持不變，這意味著這個例子是彈性碰撞。

• 小粒子與原子的碰撞也是彈性碰撞的一個例子。

• 一個男孩在地面上踢足球是非彈性碰撞的一個例子。

• 一個泥球扔到牆上粘在牆上，這是非彈性碰撞。

• 如果兩輛汽車相互碰撞，則是非彈性碰撞的一個例子。

• 如果一個粘土球從一定高度掉落，它也會由於非彈性碰撞而粘住。

結論

本碰撞教程可以看作是線性動量守恆的應用。物理學中的各種技術已經利用這些概念來更好地理解碰撞。

常見問題

Q1. 公共汽車撞到樹上是哪種型別的碰撞？

答：在這個例子中，動能(KE)不恆定，所以是非彈性碰撞。

Q2. 在非彈性碰撞中，動能是恆定的嗎？

答：不，在非彈性碰撞中，動能(KE)永遠不可能守恆或恆定。

Q3. 在非彈性碰撞的情況下，動量是恆定的嗎？

答：是的，在非彈性碰撞中，動量是恆定的。

Q4. 定義動量守恆。

答：根據動量守恆定律，碰撞前的動量之和與碰撞後的總動量相同。

Q5. 有些物體粘在其他物體上，這是哪種型別的碰撞？

答：非彈性碰撞