C++程式查詢二叉搜尋樹中兩個節點之間的最短距離

在這篇文章中，我們給定一個BST（二叉搜尋樹），我們需要找到BST中兩個給定節點之間的最短距離。讓我們來看一個樹，以下是幾種情況。

讓我們假設一些簡單的輸入和輸出場景


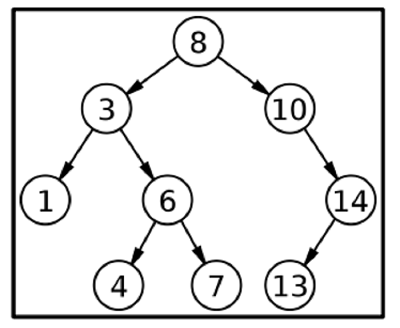
現在我們必須找到節點4和13之間的距離。

int key1=13, key2=4;
res = solve(root, min(key1,key2), max(key1,key2));
output = 6

最短距離是6，路徑是4->6->3->8->10->14->13（箭頭表示路徑定義，僅此而已）。

讓我們在上面的圖中找到來自兩個不同節點的另一個距離。考慮從節點7到節點14的距離。(6->3->8->10->14)，同樣，這裡的箭頭定義了路徑。這裡最短距離是5。

Int key1=7, key2=14;
res = solve(root, min(key1,key2), max(key1,key2));
output = 5

因此，BST中最短的距離肯定包含LCA（最近公共祖先）。所以在給定的例子中，LCA是8。所以我們可以找到節點4與8的距離，節點13與8的距離，然後將它們加起來。所以在這個問題中，我們必須找到給定兩個節點的LCA。現在，為了在BST中找到LCA，我們可以檢查以下條件：

  • 如果兩個值都小於根，則LCA在左側

  • 如果兩個值都大於根，則LCA在右側

  • 如果一個值小於根，另一個值大於根，則該節點是LCA

演算法

在二叉搜尋樹的情況下，查詢距離比其他樹快一些。以下是執行所需任務的演算法/步驟：

  • 步驟1 - 以二叉搜尋樹和兩個節點作為輸入，推匯出一個方法來查詢這兩個節點之間的距離。

  • 步驟2 - 在三種情況下計算距離

    • 如果一個節點在左子樹中，另一個節點在右子樹中，則計算左側節點的深度（從根到該節點的距離），並將其新增到右側節點的深度。

    • 如果兩個節點都在左子樹中，則將根的左孩子作為新的根，並計算左節點的深度，然後將其新增到右節點相對於新根的深度。遞迴地找到根，直到一個節點在左子樹中，另一個節點在右子樹中。

    • 同樣，如果兩個節點都在右子樹中，則遞迴地將根的右孩子作為新的根，並計算左節點的深度，然後將其新增到右節點相對於新根的深度。

  • 步驟3 - 得到的結果將是這兩個節點之間的距離。

示例

下面的C++實現查詢二叉搜尋樹中兩個節點之間的最短距離：

#include <iostream>
using namespace std;
class Node {
   public:
   int val;
   Node *left, *right;
   Node(int val) {
      this->val = val;
      left = right = NULL;
   }
};
int distance(Node* root, int val) {
   if(root->val == val) return 0;
      else if(root->val > val) return 1+distance(root->left, val);
   else return 1+distance(root->right, val);
}
int solve(Node* root, int key1, int key2) {
   if(root->val > key1 && root->val < key2) {
      return distance(root, key1) + distance(root, key2);
   } else if(root->val > key1 && root->val > key2) {
      return solve(root->left, key1, key2);
   } else {
      return solve(root->right, key1, key2);
   }
}
int main() {
   Node* root = new Node(8);
   root->left = new Node(3);
   root->right = new Node(10);
   root->left->left = new Node(1);
   root->left->right = new Node(6);
   root->right->right = new Node(14);
   root->left->right->left = new Node(4);
   root->left->right->right = new Node(7);
   root->right->right->left = new Node(13);
   int key1=13, key2=4;
   cout << solve(root, min(key1,key2), max(key1,key2));
   return 0;
}

輸出

6

結論

程式碼假設輸入正確，並且key1和key2有效。對於無效輸入，我們可以使root等於NULL並顯示自定義訊息。演算法的時間複雜度為O(h)，其中h是樹的高度。

更新於：2022年8月10日

727 次檢視

啟動你的職業生涯

完成課程獲得認證

開始學習
廣告