資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究從給定的中序和前序遍歷構造樹 (C++)
給定二叉樹的中序和前序遍歷，目標是從給定的遍歷中構造一棵樹。
中序遍歷 - 在這種型別的樹遍歷中，先訪問左子樹，然後訪問節點，最後訪問右子樹。
中序遍歷（樹根）
遍歷根節點指向的左子樹，呼叫中序遍歷(root→left)
訪問根節點
遍歷根節點指向的右子樹，呼叫中序遍歷(root→right)
前序遍歷 - 在這種型別的樹遍歷中，先訪問節點，然後訪問左子樹，最後訪問右子樹。
前序遍歷（樹根）
- 訪問根節點
- 遍歷根節點指向的左子樹，呼叫中序遍歷(root→left)
- 遍歷根節點指向的右子樹，呼叫中序遍歷(root→right)
下面給出了樹的中序和前序遍歷：
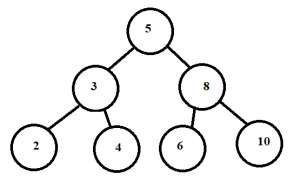
中序遍歷
2-3-4-5-6-8-10
前序遍歷
4-3-2-5-8-6-10
現在我們將根據給定的前序和中序遍歷再次構造上面的樹。
中序遍歷
2-3-4-5-6-8-10
前序遍歷
5-3-2-4-8-6-10
我們知道前序遍歷首先訪問根節點，因此第一個值始終表示樹的根。從上面的序列中，5 是樹的根。
前序遍歷
5 -3-2-4-8-6-10
從上面的中序遍歷中，我們知道節點的左子樹在它之前被遍歷，然後是它的右子樹。因此，中序遍歷中 5 左側的所有值都屬於它的左子樹，右側的所有值都屬於它的右子樹。
中序遍歷
2-3-4 ← 5 → 6-8-10
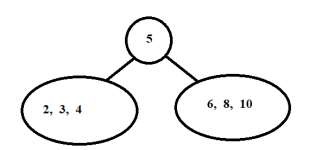
- 現在對左子樹做同樣的操作。
左子樹的前序遍歷是 3 - 2 - 4。所以 3 成為根。
中序遍歷進一步細分為 2 ← 3 → 4
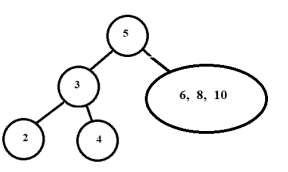
- 現在對右子樹做同樣的操作。
右子樹的前序遍歷是 8 - 6 - 10。所以 8 成為根。
中序遍歷進一步細分為 6 ← 8 → 10
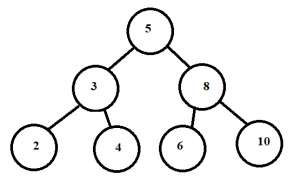
因此，透過這種方式，我們從給定的前序和中序遍歷構造了原始樹。
更新於：2020年8月3日
808 次瀏覽
廣告